题目内容
 如图,在△ABC中,AD、BE分别是BC、AC边上的高,∠C=60°,求证:
如图,在△ABC中,AD、BE分别是BC、AC边上的高,∠C=60°,求证:(1)△DCE∽△ACB;
(2)DE=
| 1 |
| 2 |
考点:相似三角形的判定
专题:立体几何
分析:(1)由AD、BE分别是BC、AC边上的高,可得∠ADB=∠BEA=90°,结合∠EOA=∠DOB,可得:△AOE∽△BOD,进而EO:DO=AO:BO,再由∠EOD=∠AOB,可得:△AOB∽△EOD,进而得到∠BED=∠DAB,再由∠ACB=∠DCE=60°,可得:△DCE∽△ACB;
(2)由∠DCE=60°,可得:△DCE与△ACB的相似比为1:2,进而得到DE=
AB.
(2)由∠DCE=60°,可得:△DCE与△ACB的相似比为1:2,进而得到DE=
| 1 |
| 2 |
解答:
证明:(1)∵△ABC中,AD、BE分别是BC、AC边上的高,
∴∠ADB=∠BEA=90°,
又∵∠EOA=∠DOB,
∴△AOE∽△BOD,
∴EO:DO=AO:BO,
又∵∠EOD=∠AOB,
∴△AOB∽△EOD,
∴∠BED=∠DAB,
∴∠ABC=90°-∠DAB=∠DEC,
又∵∠ACB=∠DCE=60°,
∴△DCE∽△ACB;
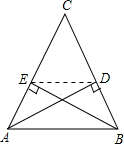
(2)∵∠DCE=60°,
故在Rt△ACD中,CD=
AC,
故
=
=
=2,
即DE=
AB
∴∠ADB=∠BEA=90°,
又∵∠EOA=∠DOB,
∴△AOE∽△BOD,
∴EO:DO=AO:BO,
又∵∠EOD=∠AOB,
∴△AOB∽△EOD,
∴∠BED=∠DAB,
∴∠ABC=90°-∠DAB=∠DEC,
又∵∠ACB=∠DCE=60°,
∴△DCE∽△ACB;

(2)∵∠DCE=60°,
故在Rt△ACD中,CD=
| 1 |
| 2 |
故
| CD |
| CA |
| CE |
| CB |
| DE |
| AB |
即DE=
| 1 |
| 2 |
点评:本题考查的知识点是相似三角形的判定与性质,熟练掌握相似三角形的判定与性质,是解答的关键.

练习册系列答案
 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
下列函数中,在其定义域内既是奇函数又是减函数的是( )
A、y=
| ||||||||
B、f(x)=
| ||||||||
C、y=
| ||||||||
| D、y=lg|x| |
若点O是△ABC的外心,且
+
+
=
,则△ABC的内角C为( )
| OA |
| OB |
| CO |
| 0 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 对某班学生一次英语测试的成绩分析,各分数段的分布如图(分数取整数),由此,估计这次测验的优秀率(不小于80分)为
对某班学生一次英语测试的成绩分析,各分数段的分布如图(分数取整数),由此,估计这次测验的优秀率(不小于80分)为