Question

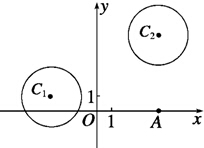在平面直角坐标系xOy中，已知圆C₁：（x+3）²+（y-1）²=4和圆C₂：（x-4）²+（y-5）²=4．
（1）判断两圆的位置关系，并求连心线的方程；
（2）求直线m的方程，使直线m被圆C₁截得的弦长为4，被圆C₂截得的弦长为2．

Answer 1

考点：圆与圆的位置关系及其判定

专题：直线与圆

分析：（1）圆C₁的圆心C₁（-3，1），r₁=2，圆C₂的圆心C₂（4，5），r₂=2．由此能判断两圆位置关系，并能求出连心线所在直线方程．
（2）由已知得直线m过圆C₁的圆心C₁（-3，1）．设直线m的方程为y-1=k（x+3）．由此能求出直线方程．

解答： 解：（1）圆C₁的圆心C₁（-3，1），r₁=2，
圆C₂的圆心C₂（4，5），r₂=2．
∴|C₁C₂|=

72+42

=

65

＞r₁+r₂，
∴两圆相离，连心线所在直线方程为：4x-7y+19=0．
（2）直线m的斜率显然存在．∵直线m被圆C₁截得弦长为4．
∴直线m过圆C₁的圆心C₁（-3，1）．
∴设直线m的方程为y-1=k（x+3）．
∴C₂（4，5）到直线m的距离：
d=

|7k-4|

k2+1

=

3

，∴k=

28± 186

46

．
∴直线方程为y-1=

28± 186

46

（x+3）．

点评：本题考查两圆位置关系的判断，考查直线方程的求法，解题时要认真审题，注意两点间距离公式的合理运用．