题目内容
求函数y=3 -x2+2x+3的定义域、值域．
考点：函数的值域,函数的定义域及其求法
专题：函数的性质及应用
分析：定义域就是使原函数有意义，显然原函数定义域为R；要求原函数的值域，先求函数-x2+2x+3的值域为（-∞，4]，根据指数函数y=3t的单调性即可求出原函数的值域．
解答：
解：使原函数有意义则x∈R，∴原函数定义域为R；
令t=-x2+2x+3，则原函数y=3t，
∵-x2+2x+3=-（x-1）2+4≤4，
∴t∈（-∞，4]
又∵指数函数y=3t，t∈（-∞，4]单调递增，
∴3-x2+2x+3≤34=81，且3-x2+2x+3＞0；
∴原函数的值域是（0，81]．
令t=-x2+2x+3，则原函数y=3t，
∵-x2+2x+3=-（x-1）2+4≤4，
∴t∈（-∞，4]
又∵指数函数y=3t，t∈（-∞，4]单调递增，
∴3-x2+2x+3≤34=81，且3-x2+2x+3＞0；
∴原函数的值域是（0，81]．
点评：考查函数的定义域，二次函数的值域，复合函数的值域，指数函数的值域．
练习册系列答案
相关题目
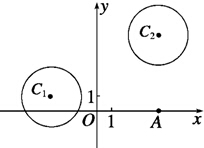在平面直角坐标系xOy中，已知圆C1：（x+3）2+（y-1）2=4和圆C2：（x-4）2+（y-5）2=4．