题目内容

圆锥底面半径是6，轴截面顶角是直角，过两条母线的截面截取地面圆周的
1
6
，求截面面积．
考点：旋转体（圆柱、圆锥、圆台）
专题：空间位置关系与距离
分析：由已知可得圆锥的母线长l=6
2
，则截面为腰长为6
2
，底面长为6的等腰三角形，求出三角形的高，代入三角形面积公式，可得答案．
解答： 解：∵圆锥底面半径是6，轴截面顶角是直角，
故圆锥的母线长l=SA=SB=6
2
，
过两条母线的截面截取地面圆周的
1
6
，
则截面为等腰三角形，底面边长AB=r=6，
如下图所示：
则三角形的高SC=
(6
2
)2-(
6
2
)2
=3
7
，
故截面面积S=
1
2
•AB•SC=9
7
点评：本题考查的知识点是旋转体，三角形面积，其中根据已知分析出截面的形状是解答的关键．
练习册系列答案
相关题目
已知关于x的方程x2+2mx+m+2=0．
（1）m为何值时，方程有实根？
（2）m为何值时，方程有一正一负两实根？
（3）m为何值时，方程有两正实根？
（4）m为何值时，方程有一实根大于1，一实根小于1？
已知a、b、c分别是△ABC的三个内角A、B、C所对的边．
（Ⅰ）若如果a、b、c成等差数列，∠B=30°，△ABC的面积为
3
2
，求b．
（Ⅱ）若a=ccosB，且b=csinA，试判断△ABC的形状．
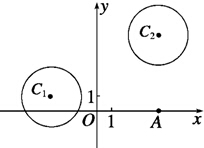在平面直角坐标系xOy中，已知圆C1：（x+3）2+（y-1）2=4和圆C2：（x-4）2+（y-5）2=4．
（1）判断两圆的位置关系，并求连心线的方程；
（2）求直线m的方程，使直线m被圆C1截得的弦长为4，被圆C2截得的弦长为2．
有一直角过道，两部分的过道宽分别为1米和3
3
米，若一根竹竿在水平放置时能通过该过道，求竹竿的长度的最大值．
在△ABC中，三个内角A，B，C对边分别为a，b，c，求证：
cosB
cosC
=
c-b•cosA
b-c•cosA
．
圆台的上底半径为2，下底半径为3，截得此圆台的圆锥的高为6，则此圆台的体积为
 
．
函数y=
x2+x+1
x2+x+3
的值域为
 
．
已知集合A={x|-2＜x＜-1，或x＞1}，B={x|x2+ax+b≤0，a，b∈R}，若A∪B={x|x＞-2}，A∩B={x|1＜x≤3}，则a=
 
，b=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网