题目内容
一条光线从点M（5，3）射出，遇x轴后反射，反射光线过点N（2，6），则反射光线所在的直线方程是 ．
考点：与直线关于点、直线对称的直线方程
专题：直线与圆
分析：由题意可得，点M（5，3）关于x轴的对称点K（5，-3）在反射光线所在的直线上，再根据反射光线过点N（2，6），则由两点式求得反射光线所在的直线方程．
解答：
解：由题意可得，点M（5，3）关于x轴的对称点K（5，-3）在反射光线所在的直线上，
再根据反射光线过点N（2，6），则由两点式求得反射光线所在的直线方程是
=
，化简可得3x+y-18=0，
故答案为：3x+y-18=0．
再根据反射光线过点N（2，6），则由两点式求得反射光线所在的直线方程是
| y+3 |
| 6+3 |
| x-5 |
| 2-5 |
故答案为：3x+y-18=0．
点评：本题主要考查用两点式求直线的方程，求一个点关于某直线的对称点的坐标的方法，利用了垂直、和中点在对称轴上这两个条件，属于基础题．
练习册系列答案
中考利剑中考试卷汇编系列答案
教育世家状元卷系列答案
黄冈课堂作业本系列答案
相关题目
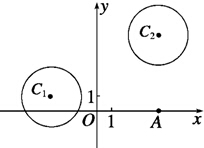在平面直角坐标系xOy中，已知圆C1：（x+3）2+（y-1）2=4和圆C2：（x-4）2+（y-5）2=4．