题目内容
已知等差数列{an}的公差不为0,前四项和S4=14,且a1,a3,a7成等比.
(1)求数列{an}的通项公式;
(2)另bn=2nan,求b1+b2+…+bn;
(3)设Tn为数列{
}的前n项和,若Tn≤λan+1对一切n∈N+恒成立,求实数λ的最小值.
(1)求数列{an}的通项公式;
(2)另bn=2nan,求b1+b2+…+bn;
(3)设Tn为数列{
| 1 |
| anan+1 |
考点:数列的求和,等差数列的性质
专题:等差数列与等比数列
分析:(1)由已知条件利用等差数列通项公式和前n项和公式及等比数列性质,求出首项和公差,由此能求出an=n+1.
(2)由bn=2nan=2n(n+1),利用错位相减法能求出b1+b2+…+bn=n•2n.
(3)由
=
=
-
,利用裂项求和法能求出λ的最小值.
(2)由bn=2nan=2n(n+1),利用错位相减法能求出b1+b2+…+bn=n•2n.
(3)由
| 1 |
| anan+1 |
| 1 |
| (n+1)(n+2) |
| 1 |
| n+1 |
| 1 |
| n+2 |
解答:
解:(1)∵等差数列{an}的公差不为0,
前四项和S4=14,且a1,a3,a7成等比,
∴
,
解得d=1,或d=0(舍),
∴a1=2,∴an=n+1.
(2)∵bn=2nan=2n(n+1),
记Sn=b1+b2+…+bn,
则Sn=2×2+22×3+23×4+…+2n(n+1),①
2Sn=22×2+23×3+…+2n+1×(n+1),②
①-②,得:-Sn=2×2+22+23+…+2n-2n+1•(n+1)
=4+
-2n+1•(n+1),
∴Sn=n•2n
∴b1+b2+…+bn=n•2n.
(3)∵
=
=
-
,
∴Tn=
-
+
-
+…+
-
=
-
=
,
∵Tn≤λan+1,∴λ≥
,
又
=
≤
,
∴λ的最小值为
.…(12分)
前四项和S4=14,且a1,a3,a7成等比,
∴
|
解得d=1,或d=0(舍),
∴a1=2,∴an=n+1.
(2)∵bn=2nan=2n(n+1),
记Sn=b1+b2+…+bn,
则Sn=2×2+22×3+23×4+…+2n(n+1),①
2Sn=22×2+23×3+…+2n+1×(n+1),②
①-②,得:-Sn=2×2+22+23+…+2n-2n+1•(n+1)
=4+
| 4(1-2n-1) |
| 1-2 |
∴Sn=n•2n
∴b1+b2+…+bn=n•2n.
(3)∵
| 1 |
| anan+1 |
| 1 |
| (n+1)(n+2) |
| 1 |
| n+1 |
| 1 |
| n+2 |
∴Tn=
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n+1 |
| 1 |
| n+2 |
| 1 |
| 2 |
| 1 |
| n+2 |
| n |
| 2(n+2) |
∵Tn≤λan+1,∴λ≥
| n |
| 2(n+2)2 |
又
| n |
| 2(n+2)2 |
| 1 | ||
2(n+
|
| 1 |
| 16 |
∴λ的最小值为
| 1 |
| 16 |
点评:本题考查数列的通项公式的求法,考查数列的前n项和的求法,考查实数的最小值的求法,解题时要认真审题,注意裂项求和法的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=2cos2x+6sinx+1的最大值为( )
| A、10 | B、9 | C、8 | D、7 |
已知集合M={x|-1<x≤1},N={x|1≤2x<4},则M∩N( )
| A、{x|-1<x<1} |
| B、{x|0≤x<1} |
| C、{x|0≤x≤1} |
| D、{x|-1<x<2} |
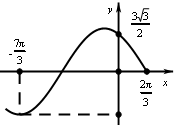 已知ω>0,-π<φ<π,函数f(x)=Asin(ωx+φ)的部分图象如图所示,则f(x)解析式为( )
已知ω>0,-π<φ<π,函数f(x)=Asin(ωx+φ)的部分图象如图所示,则f(x)解析式为( )A、f(x)=3sin(
| ||||
B、f(x)=3sin(
| ||||
C、f(x)=3sin(
| ||||
D、f(x)=3sin(2x+
|
如果a>b>0,那么下列不等式成立的是( )
A、
| ||||
| B、a2<b2 | ||||
| C、log2a<log2b | ||||
D、(
|
 某英语学习小组共12名同学进行英语听力测试,随机抽取6名同学的测试成绩(单位:分),用茎叶图记录如下,其中茎为十位数,叶为个位数.
某英语学习小组共12名同学进行英语听力测试,随机抽取6名同学的测试成绩(单位:分),用茎叶图记录如下,其中茎为十位数,叶为个位数.