题目内容
 某英语学习小组共12名同学进行英语听力测试,随机抽取6名同学的测试成绩(单位:分),用茎叶图记录如下,其中茎为十位数,叶为个位数.
某英语学习小组共12名同学进行英语听力测试,随机抽取6名同学的测试成绩(单位:分),用茎叶图记录如下,其中茎为十位数,叶为个位数.(1)根据茎叶图计算样本均值;
(2)成绩高于样本均值的同学为优秀,根据茎叶图估计该小组12名同学中有几名优秀同学;
(3)从该小组12名同学中任取2人,求仅有1人是来自随机抽取6人中优秀同学的概率.
考点:古典概型及其概率计算公式,茎叶图
专题:概率与统计
分析:(1)依题意,这6个同学的将成绩从小到大依次为18,19,21,22,28,30,根据公式如果有n个数x1,x2,x3,…xn那么这n个数的平均数
=
求出样本均值;
(2)由于这6个同学的成绩高于样本均值的有2名,故估计该小组12名同学中优秀的人数为12×
=4名;
(3)从该小组12名同学中,任取2人有
=66种方法,而恰有1名优秀同学有
=20种方法,根据古典概型共是可求得仅有1人是来自随机抽取6人中优秀同学的概率.
. |
| x |
| x1+x2+x3+…+xn |
| n |
(2)由于这6个同学的成绩高于样本均值的有2名,故估计该小组12名同学中优秀的人数为12×
| 2 |
| 6 |
(3)从该小组12名同学中,任取2人有
| C | 2 12 |
| C | 1 10 |
| C | 1 2 |
解答:
解:(1)由题意可知,样本均值
=
=23(4分)
(2)∵样本中成绩高于样本均值的同学共有2名,
∴可以估计该小组12名同学中优秀同学的人数为:12×
=4(8分)
(3)∵从该小组12名同学中,任取2人有
=66种方法,
而恰有1名优秀同学有
=20
∴所求的概率为:P=
=
=
(12分)
. |
| x |
| 18+19+21+22+28+30 |
| 6 |
(2)∵样本中成绩高于样本均值的同学共有2名,
∴可以估计该小组12名同学中优秀同学的人数为:12×
| 2 |
| 6 |
(3)∵从该小组12名同学中,任取2人有
| C | 2 12 |
而恰有1名优秀同学有
| C | 1 10 |
| C | 1 2 |
∴所求的概率为:P=
| ||||
|
| 20 |
| 66 |
| 10 |
| 33 |
点评:本题考查的知识点是古典概型概率计算公式,其中熟练掌握利用古典概型概率计算公式求概率的步骤,是解答的关键.

练习册系列答案
相关题目
在边长为3的正方形ABCD内随机取一点,取到的点到顶点A的距离大于1的概率是( )
A、
| ||
B、1-
| ||
C、
| ||
D、1-
|
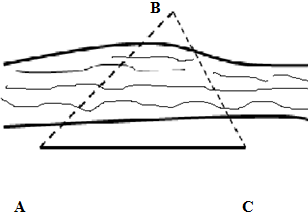 如图,在一次测量活动中,要测量河两岸B、C两点间的距离,测量者在河的一侧,测得AC=24m,∠BAC=45°,∠ACB=75°,求B、C两点间的距离.
如图,在一次测量活动中,要测量河两岸B、C两点间的距离,测量者在河的一侧,测得AC=24m,∠BAC=45°,∠ACB=75°,求B、C两点间的距离.