题目内容
射击比赛中,每位射手射击队10次,每次一发,击中目标得3分,未击中目标得0分,每射击一次,凡参赛者加2分,已知小李击中目标的概率为0.8.
(1)设X为小李击中目标的次数,求X的概率分布;
(2)求小李在比赛中的得分的数学期望与方差.
(1)设X为小李击中目标的次数,求X的概率分布;
(2)求小李在比赛中的得分的数学期望与方差.
考点:离散型随机变量的期望与方差,离散型随机变量及其分布列
专题:应用题,概率与统计
分析:(1)利用查n次独立重复实验中恰好发生k次的概率公式,可得X的概率分布;
(2)设小李在比赛中的得分为Y,由(1)知满足二项分布X~B(10,0.8),即可求小李在比赛中的得分的数学期望与方差.
(2)设小李在比赛中的得分为Y,由(1)知满足二项分布X~B(10,0.8),即可求小李在比赛中的得分的数学期望与方差.
解答:
解:(1)X的概率分布为
(2)设小李在比赛中的得分为Y,由(1)知满足二项分布X~B(10,0.8)
所以E(Y)=E(3X+2)=3E(X)+2=3×10×0.8+2=26,
D(Y)=D(3X+2)=9D(X)=9×10×0.8×0.2=14.4,
| X | O | 1 | … | 10 | ||
| P | 0.210 |
| … | 0.810 |
所以E(Y)=E(3X+2)=3E(X)+2=3×10×0.8+2=26,
D(Y)=D(3X+2)=9D(X)=9×10×0.8×0.2=14.4,
点评:本题主要考查n次独立重复实验中恰好发生k次的概率,考查离散型随机变量的分布列的数学期望的求法,解题时要认真审题,注意二项分布的合理运用.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
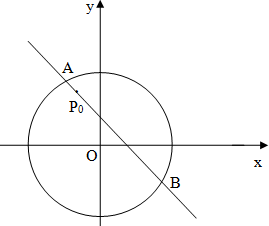 如图,圆x2+y2=8内有一点P0(-1,2),AB为过点P0且倾斜角为α的弦.
如图,圆x2+y2=8内有一点P0(-1,2),AB为过点P0且倾斜角为α的弦.