Question

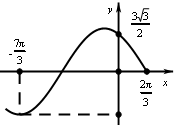已知ω＞0，-π＜φ＜π，函数f（x）=Asin（ωx+φ）的部分图象如图所示，则f（x）解析式为（　　）

• A、f（x）=3sin（

  1

  2

  x+

  2π

  3

  ）
• B、f（x）=3sin（

  1

  2

  x-

  π

  3

  ）
• C、f（x）=3sin（

  1

  2

  x+

  π

  3

  ）
• D、f（x）=3sin（2x+

  π

  3

  ）

Answer 1

考点：由y=Asin（ωx+φ）的部分图象确定其解析式

专题：三角函数的图像与性质

分析：由图易知T=4π，可求得ω=

1

2

；又

2π

3

ω+φ=2kπ+π（k∈Z），-π＜φ＜π，由此可求得φ=

2π

3

；再由f（0）=

3 3

2

可求得A，从而可得答案．

解答： 解：由图知，

3

4

T=

2π

3

-（-

7π

3

）=3π，又ω＞0，
∴T=

2π

ω

=4π，
∴ω=

1

2

；
又

2π

3

ω+φ=2kπ+π（k∈Z），
∴φ=2kπ+π-

π

3

=2kπ+

2π

3

（k∈Z），
又-π＜φ＜π，
∴φ=

2π

3

；
又f（0）=Asin

2π

3

=

3

2

A=

3 3

2

，
∴A=3；
∴f（x）=3sin（

1

2

x+

2π

3

），
故选：A．

点评：本题考查由y=Asin（ωx+φ）的部分图象确定其解析式，确定φ是关键，确定A是难点，考查识图及运算求解能力，属于中档题．