题目内容
19.若直线2ax-by+2=0(a,b∈R)始终平分圆x2+y2+2x-4y+1=0的周长,则ab的最大值是$\frac{1}{4}$.分析 化圆的方程为标准式,求出圆心坐标,由题意可得直线过圆心,得到a+b=1,然后利用基本不等式求最值.
解答 解:化x2+y2+2x-4y+1=0为(x+1)2+(y-2)2=4.
∴圆心坐标为(-1,2),
∵直线2ax-by+2=0(a,b∈R)始终平分圆x2+y2+2x-4y+1=0的周长,
∴直线2ax-by+2=0过圆心,则-2a-2b+2=0,即a+b=1.
∴当a,b大于0时,且a=b,ab有最大值为$(\frac{a+b}{2})^{2}=(\frac{1}{2})^{2}=\frac{1}{4}$.
故答案为:$\frac{1}{4}$.
点评 本题考查直线与圆位置关系的应用,训练了利用基本不等式求最值,是基础题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
9.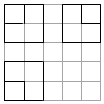 如图,正方形网格中,粗实线画出的是某几何体的三视图,若该几何体的体积为7,则该几何体的表面积为( )
如图,正方形网格中,粗实线画出的是某几何体的三视图,若该几何体的体积为7,则该几何体的表面积为( )
 如图,正方形网格中,粗实线画出的是某几何体的三视图,若该几何体的体积为7,则该几何体的表面积为( )
如图,正方形网格中,粗实线画出的是某几何体的三视图,若该几何体的体积为7,则该几何体的表面积为( )| A. | 18 | B. | 21 | C. | 24 | D. | 27 |
10.福利彩票“双色球”中红色球的号码由编号为01,02,…,33的33个个体组成,小明利用下面的随机数表选取6组数作为6个红色球的编号,选取方法是从随机数表第1行的第7列数字开始由左到右依次读取数据,则选出来的第3个红色球的编号为( )
| 49 54 43 54 15 37 17 93 39 78 87 35 20 96 43 84 17 34 91 64 |
| 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 76 |
| A. | 06 | B. | 17 | C. | 20 | D. | 24 |
7.已知$α∈(\frac{π}{3},π)$,且$sin(α+\frac{π}{6})=\frac{3}{5}$,则cosα=( )
| A. | $\frac{{3-4\sqrt{3}}}{10}$ | B. | $\frac{{3+4\sqrt{3}}}{10}$ | C. | $\frac{{-3-4\sqrt{3}}}{10}$ | D. | $\frac{{-3+4\sqrt{3}}}{10}$ |
4.执行如图2所示的程序框图,若输出S=7,则输入k(k∈N*)的值为( )

| A. | 2 | B. | 3 | C. | 4 | D. | 5 |