题目内容
14．已知函数f（x）=|2x-1|-|x-3|．（Ⅰ）解不等式f（x）≥1；
（Ⅱ）当-9≤x≤4时，不等式f（x）＜a成立，求实数a的取值范围．
分析 （Ⅰ）通讨论x的范围，得到关于x的不等式组，解出即可；（Ⅱ）通过讨论x的范围，求出各个区间上的f（x）的最大值，求出a的范围即可．
解答 解：（Ⅰ）∵|2x-1|-|x-3|≥1，
∴$\left\{\begin{array}{l}{x≥3}\\{2x-1-x+3≥1}\end{array}\right.$或$\left\{\begin{array}{l}{\frac{1}{2}＜x＜3}\\{2x-1+x-3≥1}\end{array}\right.$或$\left\{\begin{array}{l}{x≤\frac{1}{2}}\\{1-2x+x-3≥1}\end{array}\right.$，
解得：x≥$\frac{5}{3}$或x≤-3，
故不等式的解集是：$（-∞，-3]∪[\frac{5}{3}，+∞）$．
（Ⅱ）f（x）=|2x-1|-|x-3|，
x≥3时，f（x）=x+2，f（x）的最大值是f（4）=5，
$\frac{1}{2}$≤x≤3时，f（x）=3x-4，f（x）的最大值是f（3）=5，
-9≤x≤$\frac{1}{2}$时，f（x）=-x-2，f（x）的最大值是f（-9）=7，
当-9≤x≤4时，不等式f（x）＜a成立，
则a＞7，
即a∈（7，+∞）．
点评 本题考查了解绝对值不等式问题，考查分类讨论思想，转化思想，是一道中档题．
练习册系列答案
核心素养学练评系列答案
单元期中期末卷系列答案
相关题目
5．
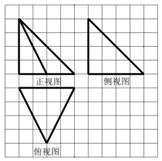如图，网络纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则在该几何体中，最长的棱的长度是（ ）
如图，网络纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则在该几何体中，最长的棱的长度是（ ）| A． | 4 | B． | 2$\sqrt{5}$ | C． | 4$\sqrt{2}$ | D． | 6 |
6．已知l、m表示直线，α、β、γ表示平面，下列条件中能推出结论正确的选项是（ ）
条件：①l?α，α∥β；②α∥β，β∥γ；③l⊥α，α∥β；④l⊥m，l⊥α，m⊥β．
结论：a：l⊥β；b：α⊥β；c：l∥β；d：α∥γ．
条件：①l?α，α∥β；②α∥β，β∥γ；③l⊥α，α∥β；④l⊥m，l⊥α，m⊥β．
结论：a：l⊥β；b：α⊥β；c：l∥β；d：α∥γ．
| A． | ①⇒c、②⇒d、③⇒a、④⇒b | B． | ①⇒a、②⇒d、③⇒c、④⇒b | C． | ①⇒b、②⇒d、③⇒a、④⇒c | D． | ①⇒c、②⇒b、③⇒a、④⇒d |
3．已知函数f（x）=$\left\{\begin{array}{l}{-x+1，}&{x＜1}\\{{2}^{x}-2，}&{x≥1}\end{array}\right.$，g（x）=$\frac{1}{x}$，若对任意x∈[m，+∞）（m＞0），总存在两个x0∈[0，2]，使得f（x0）=g（x），则实数m的取值范围是（ ）
| A． | [1，+∞） | B． | （0，1] | C． | [$\frac{1}{2}$，+∞） | D． | （0，$\frac{1}{2}$] |