题目内容
1.设f(x)=1g$\frac{1+{2}^{x}+{3}^{x}+{4}^{x}•a}{4}$,其中a是实数,若f(x)当x∈(-∞,1]时有意义,求a的取值范围.分析 由题意可得,当x∈(-∞,1]时,$\frac{1+{2}^{x}+{3}^{x}+{4}^{x}•a}{4}$>0,即当x∈(-∞,1]时,a•4x+3x+2x+1>0,分离参数a,利用函数的单调性求出g(x)=-[$(\frac{3}{4})^{x}+(\frac{1}{2})^{x}+(\frac{1}{4})^{x}$]在x∈(-∞,1]上的最大值得答案.
解答 解:由题意可知,当x∈(-∞,1]时,$\frac{1+{2}^{x}+{3}^{x}+{4}^{x}•a}{4}$>0,
即当x∈(-∞,1]时,a•4x+3x+2x+1>0,
∴a>-[$(\frac{3}{4})^{x}+(\frac{1}{2})^{x}+(\frac{1}{4})^{x}$]在x∈(-∞,1]上恒成立.
∵函数g(x)=-[$(\frac{3}{4})^{x}+(\frac{1}{2})^{x}+(\frac{1}{4})^{x}$]在x∈(-∞,1]上为增函数,
∴$g(x)_{max}=g(1)=-\frac{3}{2}$.
∴$a>-\frac{3}{2}$.
故a的取值范围为($-\frac{3}{2},+∞$).
点评 本题考查函数的定义域及其求法,考查数学转化思想方法,是中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
9.函数y=|log3x|的图象与直线l1:y=m从左至右分别交于点A,B,与直线${l_2}:y=\frac{8}{2m+1}(m>0)$从左至右分别交于点C,D.记线段AC和BD在x轴上的投影长度分别为a,b,则$\frac{b}{a}$的最小值为( )
| A. | $81\sqrt{3}$ | B. | $27\sqrt{3}$ | C. | $9\sqrt{3}$ | D. | $3\sqrt{3}$ |
16.将函数y=f(x)的图象上的所有点向左平行移动$\frac{π}{10}$个单位长度,再把所得各点的横坐标伸长为原来的2倍(纵坐标不变),所得图象的函数解析式为y=cosx,则y=f(x)是( )
| A. | 周期为4π的奇函数 | B. | 周期为4π的偶函数 | ||
| C. | 周期为π的奇函数 | D. | 周期为π的非奇非偶函数 |
13.在《九章算术》中有一个古典名题“两鼠穿墙”问题:今有垣厚五尺,两鼠对穿,大鼠日一尺,小鼠也日一尺.大鼠日自倍,小鼠日自半,问何日相逢?大意是有厚墙五尺,两只老鼠从墙的两边分别打洞穿墙.大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半,问几天后两鼠相遇?( )
| A. | 2$\frac{2}{17}$ | B. | 2$\frac{3}{17}$ | C. | 2$\frac{5}{17}$ | D. | 2.25 |
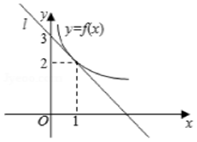 如图所示,y=f(x)是可导函数,直线l:y=kx+3是曲线y=f(x)在x=1处的切线,若h(x)=xf(x),则h(x)在x=1处的切线方程为x-y+1=0.
如图所示,y=f(x)是可导函数,直线l:y=kx+3是曲线y=f(x)在x=1处的切线,若h(x)=xf(x),则h(x)在x=1处的切线方程为x-y+1=0.