题目内容
10.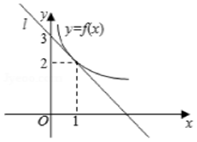 如图所示,y=f(x)是可导函数,直线l:y=kx+3是曲线y=f(x)在x=1处的切线,若h(x)=xf(x),则h(x)在x=1处的切线方程为x-y+1=0.
如图所示,y=f(x)是可导函数,直线l:y=kx+3是曲线y=f(x)在x=1处的切线,若h(x)=xf(x),则h(x)在x=1处的切线方程为x-y+1=0.
分析 由切点以及导数的关系可得f′(1)=-1,f(1)=2,由乘积的导数求导函数,代值计算可得h(x)在x=1处的切线斜率,求出h(1),由点斜式方程即可得到所求切线的方程.
解答 解:∵直线l:y=kx+3是曲线y=f(x)在x=1处的切线,
∴点(1,2)为切点,故f′(1)=k,f(1)=k+3=2,
解得k=-1,
故f′(1)=-1,f(1)=2,
由h(x)=xf(x)可得h′(x)=f(x)+xf′(x),
∴h′(1)=f(1)+f′(1)=1,h(1)=f(1)=2,
则h(x)在x=1处的切线方程为y-2=x-1,
即为x-y+1=0.
故答案为:x-y+1=0.
点评 本题考查导数的运用:求切线方程,考查导数的几何意义,运用直线方程和求导,数形结合是解决问题的关键,属基础题.

练习册系列答案
相关题目
18.已知O为坐标原点,F1、F2分别是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左右焦点,A为C的左顶点,P为C上一点,且PF1⊥x轴,过点A的直线l与线段PF1交于点M,与y轴交于点E,若直线F2M与y轴交点为N,OE=2ON,则C的离心率为( )
| A. | $\frac{1}{3}$ | B. | 2 | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
5.有两张卡片,一张的正反面分别画着老鼠和小鸡,另一张的正反面分别画着老鹰和蛇,现在有两个小孩随机地将两张卡片排在一起放在桌面上,不考虑顺序,则向上的图案是老鹰和小鸡的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
15.某种电路开关闭合后会出现红灯或绿灯闪烁,已知开关第一次闭合后出现红灯的概率为0.5,两次闭合后都出现红灯的概率为0.2,则在第一次闭合后出现红灯的条件下第二次闭合后出现红灯的概率为( )
| A. | 0.1 | B. | 0.2 | C. | 0.4 | D. | 0.5 |
19.已知集合A={x|x2+5x>0},B={x|-3<x<4},则A∩B等于( )
| A. | (-5,0) | B. | (-3,0) | C. | (0,4) | D. | (-5,4) |
20.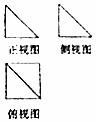 如图是一个几何体的三视图,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该多面体的各条棱中最长棱的长度为( )
如图是一个几何体的三视图,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该多面体的各条棱中最长棱的长度为( )
 如图是一个几何体的三视图,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该多面体的各条棱中最长棱的长度为( )
如图是一个几何体的三视图,其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形,则该多面体的各条棱中最长棱的长度为( )| A. | $\sqrt{7}$ | B. | $\sqrt{5}$ | C. | 2 | D. | $\sqrt{3}$ |