题目内容
13.在《九章算术》中有一个古典名题“两鼠穿墙”问题:今有垣厚五尺,两鼠对穿,大鼠日一尺,小鼠也日一尺.大鼠日自倍,小鼠日自半,问何日相逢?大意是有厚墙五尺,两只老鼠从墙的两边分别打洞穿墙.大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半,问几天后两鼠相遇?( )| A. | 2$\frac{2}{17}$ | B. | 2$\frac{3}{17}$ | C. | 2$\frac{5}{17}$ | D. | 2.25 |
分析 由于前两天大鼠打1+2尺,小鼠打1+$\frac{1}{2}$尺,因此前两天两鼠共打3+1.5=4.5.第三天,大鼠打4尺,小鼠打$\frac{1}{4}$尺,因此第三天相遇.设第三天,大鼠打y尺,小鼠打0.5-y尺,则$\frac{y}{4}$=$\frac{0.5-y}{\frac{1}{4}}$,解得y即可得出.
解答 解:由于前两天大鼠打1+2尺,小鼠打1+$\frac{1}{2}$尺,因此前两天两鼠共打3+1.5=4.5.
第三天,大鼠打4尺,小鼠打$\frac{1}{4}$尺,因此第三天相遇.
设第三天,大鼠打y尺,小鼠打0.5-y尺,
则$\frac{y}{4}$=$\frac{0.5-y}{\frac{1}{4}}$,解得y=$\frac{8}{17}$.
相见时大鼠打了1+2+$\frac{8}{17}$=3$\frac{8}{17}$尺长的洞,小鼠打了1+$\frac{1}{2}$+$\frac{1}{34}$=1$\frac{9}{17}$尺长的洞,
x=2+$\frac{2}{17}$=2$\frac{2}{17}$天,
故选:A.
点评 本题考查了等差数列与等比数列的通项公式求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案 孟建平错题本系列答案
孟建平错题本系列答案
相关题目
18.已知O为坐标原点,F1、F2分别是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左右焦点,A为C的左顶点,P为C上一点,且PF1⊥x轴,过点A的直线l与线段PF1交于点M,与y轴交于点E,若直线F2M与y轴交点为N,OE=2ON,则C的离心率为( )
| A. | $\frac{1}{3}$ | B. | 2 | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
5.有两张卡片,一张的正反面分别画着老鼠和小鸡,另一张的正反面分别画着老鹰和蛇,现在有两个小孩随机地将两张卡片排在一起放在桌面上,不考虑顺序,则向上的图案是老鹰和小鸡的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
3.执行如图所示的程序框图,若输出的结果是6,则判断框内m的取值范围是( )
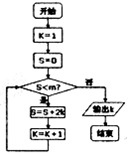

| A. | (30,42] | B. | (20,30) | C. | (20,30] | D. | (20,42) |