题目内容
11.已知函数f(x)=lnx+a(x2-x)(I)若a=-1,求f(x)的极值;
(Ⅱ)若f(x)存在单调递减区间,求a的取值范围;
(Ⅲ)若f(x)的图象与x轴交于A(x1,0),B(x2,0)(x1<x2),AB的中点为C(x0,0),求证:f′(x0)≠0.
分析 (Ⅰ)求出函数的导数,解关于导函数的方程,求出函数的单调区间,从而求出函数的极值即可;
(Ⅱ)求出函数的导数,通过讨论a的范围,得到函数的单调区间,根据函数的单调性确定a的范围即可;
(Ⅲ)根据ln$\frac{{x}_{1}}{{x}_{2}}$-$\frac{2{(x}_{1}{-x}_{2})}{{{x}_{1}+x}_{2}}$=0,得到ln$\frac{{x}_{1}}{{x}_{2}}$-$\frac{2\frac{{x}_{1}}{{x}_{2}}-2}{\frac{{x}_{1}}{{x}_{2}}+1}$=0,设t=$\frac{{x}_{1}}{{x}_{2}}$(0<t<1),则lnt-$\frac{2t-2}{t+1}$=0,令u(t)=lnt-$\frac{2t-2}{t+1}$(0<t<1),根据函数的单调性证明即可.
解答 解:(I)f(x)定义域为(0,+∞),f′(x)=$\frac{1}{x}$+2ax-a=$\frac{2{ax}^{2}-ax+1}{x}$,
当a=-1时,f′(x)=$\frac{-(2x+1)(x-1)}{x}$,由f′(x)=0,∴x=-$\frac{1}{2}$或x=1,
| x | (0,1) | 1 | (1,+∞) |
| f′(x) | + | 0 | - |
| f(x) | 单调递增 | 极大值 | 单调递减 |
(Ⅱ)f′(x)=$\frac{2{ax}^{2}-ax+1}{x}$,
∵f(x)存在单调递减区间,∴f′(x)<0在(0,+∞)内有解,
即关于x的不等式2ax2-ax+1<0在(0,+∞)内有解,
若a=0,则f′(x)=$\frac{1}{x}$>0,f(x)在(0,+∞)单调递增,不存在单调递减区间;
若a>0,则函数y=2ax2-ax+1的图象是开口向上的抛物线,且恒过点(0,1),
要使关于x的不等式2ax2-ax+1<0在(0,+∞)内有解,
则应有$\left\{\begin{array}{l}{△{=a}^{2}-8a>0}\\{-\frac{-a}{4a}>0}\end{array}\right.$,
∴a<0或a>8,由于a>0,∴a>8;
若a<0,
则函数y=2ax2-ax+1的图象是开口向下的抛物线,且恒过点(0,1),
关于x的不等式2ax2-ax+1<0在(0,+∞)内一定有解.
综上,a<0或a>8;
(Ⅲ)依题意:x1+x2=2x0,假设结论不成立,即f′(x0)=0,
则有$\left\{\begin{array}{l}{f{(x}_{1})=l{nx}_{1}+a{{(x}_{1}}^{2}{-x}_{1})=0①}\\{f{(x}_{2})=l{nx}_{2}+a{{(x}_{2}}^{2}{-x}_{2})=0②}\\{f′{(x}_{0})=\frac{1}{{x}_{0}}+2{ax}_{0}-a=0③}\end{array}\right.$,
①-②,得ln$\frac{{x}_{1}}{{x}_{2}}$+a(${{x}_{1}}^{2}$-${{x}_{2}}^{2}$)-a(x1-x2)=0,
∴ln$\frac{{x}_{1}}{{x}_{2}}$+a(x1+x2)(x1-x2)-a(x1-x2)=0,
由③得,$\frac{2}{{{x}_{1}+x}_{2}}$+a(x1+x2)-a=0,
∴ln$\frac{{x}_{1}}{{x}_{2}}$-$\frac{2{(x}_{1}{-x}_{2})}{{{x}_{1}+x}_{2}}$=0,即ln$\frac{{x}_{1}}{{x}_{2}}$-$\frac{2\frac{{x}_{1}}{{x}_{2}}-2}{\frac{{x}_{1}}{{x}_{2}}+1}$=0,
设t=$\frac{{x}_{1}}{{x}_{2}}$(0<t<1),则lnt-$\frac{2t-2}{t+1}$=0,---④
令u(t)=lnt-$\frac{2t-2}{t+1}$(0<t<1),
∴u′(t)=$\frac{{(t-1)}^{2}}{{t(t+1)}^{2}}$>0,∴u(t)在(0,1)上为增函数.
∴u(t)<u(1)=0,即lnt-$\frac{2t-2}{t+1}$<0,与④式矛盾
∴假设不成立,∴f′(x0)≠0.
点评 本题考查了函数的单调性、极值问题,考查导数的应用以及分类讨论思想、转化思想,考查不等式的证明,是一道综合题.

练习册系列答案
相关题目
11.已知全集U=R,A={x|x2-3x-4>0},B={x|-2≤x≤2},则如图所示的阴影部分所表示的集合为( )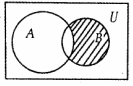

| A. | {x|-2≤x<4} | B. | {x|x≤2或x≥4} | C. | {x|-2≤x≤-1} | D. | {x|-1≤x≤2} |
2.某品牌汽车4S店对最近100位采用分期付款的购车者进行统计,统计结果如表所示:
已知分3期付款的频率为0.2,4S店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元;分2期或3期付款,其利润为1.5万元;分4期或5期付款,其利润为2万元,用Y表示经销一辆汽车的利润.
(1)求上表中a,b的值;
(2)若以频率作为概率,求事件A:“购买该品牌的3位顾客中,至多有一位采用分3期付款”的概率P(A);
(3)求Y的分布列及数学期望EY.
| 付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 40 | 20 | a | 10 | b |
(1)求上表中a,b的值;
(2)若以频率作为概率,求事件A:“购买该品牌的3位顾客中,至多有一位采用分3期付款”的概率P(A);
(3)求Y的分布列及数学期望EY.
16.若sinθ+coθ=$\frac{2}{3}$,则sinθ-cosθ=( )
| A. | $\frac{\sqrt{14}}{3}$ | B. | -$\frac{\sqrt{6}}{3}$ | C. | ±$\frac{\sqrt{14}}{3}$ | D. | ±$\frac{\sqrt{6}}{3}$ |