题目内容
9.函数y=|log3x|的图象与直线l1:y=m从左至右分别交于点A,B,与直线${l_2}:y=\frac{8}{2m+1}(m>0)$从左至右分别交于点C,D.记线段AC和BD在x轴上的投影长度分别为a,b,则$\frac{b}{a}$的最小值为( )| A. | $81\sqrt{3}$ | B. | $27\sqrt{3}$ | C. | $9\sqrt{3}$ | D. | $3\sqrt{3}$ |
分析 依题意可求得A,B,C,D的横坐标值,得$\frac{b}{a}$=$\frac{|{3}^{m}-{3}^{\frac{8}{2m+1}|}}{|{3}^{-m}-{3}^{-\frac{8}{2m+1}}|}$=${3}^{m+\frac{8}{2m+1}}$,利用基本不等式可求最小值.
解答 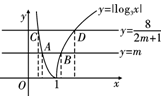 解:在同一坐标系中作出y=m,y=$\frac{8}{2m+1}$(m>0),y=|log3x|的图象,如图,设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
解:在同一坐标系中作出y=m,y=$\frac{8}{2m+1}$(m>0),y=|log3x|的图象,如图,设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
由|log3x|=m,得x1=3-m,x2=3m,
由log3x|=$\frac{8}{2m+1}$,得x3=${3}^{-\frac{8}{2m+1}}$,x4=${3}^{\frac{8}{2m+1}}$.
依照题意得$\frac{b}{a}$=$\frac{|{3}^{m}-{3}^{\frac{8}{2m+1}|}}{|{3}^{-m}-{3}^{-\frac{8}{2m+1}}|}$=${3}^{m+\frac{8}{2m+1}}$,
又m>0,∴m+$\frac{8}{2m+1}$=$\frac{1}{2}$(2m+1)+$\frac{8}{2m+1}$-$\frac{1}{2}$≥$\frac{7}{2}$,
当且仅当$\frac{1}{2}$(2m+1)=$\frac{8}{2m+1}$,即m=$\frac{3}{2}$时取“=”号,
∴$\frac{b}{a}$的最小值为27$\sqrt{3}$,
故选B.
点评 本题考查对数函数图象与性质的综合应用,理解投影的概念并能把问题转化为基本不等式求最值是解决问题的关键,属中档题.

练习册系列答案
相关题目
18.已知O为坐标原点,F1、F2分别是双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左右焦点,A为C的左顶点,P为C上一点,且PF1⊥x轴,过点A的直线l与线段PF1交于点M,与y轴交于点E,若直线F2M与y轴交点为N,OE=2ON,则C的离心率为( )
| A. | $\frac{1}{3}$ | B. | 2 | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
19.已知集合A={x|x2+5x>0},B={x|-3<x<4},则A∩B等于( )
| A. | (-5,0) | B. | (-3,0) | C. | (0,4) | D. | (-5,4) |