题目内容
16.将函数y=f(x)的图象上的所有点向左平行移动$\frac{π}{10}$个单位长度,再把所得各点的横坐标伸长为原来的2倍(纵坐标不变),所得图象的函数解析式为y=cosx,则y=f(x)是( )| A. | 周期为4π的奇函数 | B. | 周期为4π的偶函数 | ||
| C. | 周期为π的奇函数 | D. | 周期为π的非奇非偶函数 |
分析 根据函数y=Asin(ωx+∅)的图象变换规律可得f(x)=cos(2x-$\frac{π}{5}$),利用三角函数的图象和性质从而得解.
解答 解:由题意可得把函数 y=cosx 的图象的横坐标变为原来的$\frac{1}{2}$倍(纵坐标不变),再把图象上所有点向右平行移动$\frac{π}{10}$个单位长度,
可得f(x)的图象,故 f(x)=cos2(x-$\frac{π}{10}$)=cos(2x-$\frac{π}{5}$),
可得:f(x)的周期T=$\frac{2π}{2}$=π.
由于f(0)=cos(-$\frac{π}{5}$)≠0,且f(0)=cos(-$\frac{π}{5}$)≠±1,故函数f(x)为非奇非偶函数,
故选:D.
点评 本题主要考查三角函数的图象和性质,函数y=Asin(ωx+∅)的图象变换,考查了数形结合思想,属于基础题.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
11.设集合M={x|x2+3x+2>0},集合N={-2,-1,0,1,2},则M∩N=( )
| A. | {-2,-1} | B. | {0,1,2} | C. | {-1,0,1,2} | D. | {-2,-1,0,1,2} |
5.有两张卡片,一张的正反面分别画着老鼠和小鸡,另一张的正反面分别画着老鹰和蛇,现在有两个小孩随机地将两张卡片排在一起放在桌面上,不考虑顺序,则向上的图案是老鹰和小鸡的概率是( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{6}$ |
6.已知集合A={x|(x-2)(x+6)>0},B={x|-3<x<4},则A∩B等于( )
| A. | (-3,-2) | B. | (-3,2) | C. | (2,4) | D. | (-2,4) |
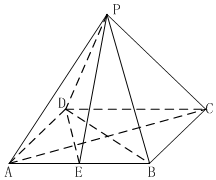 如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上E是AB的中点.
如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上E是AB的中点.