题目内容
11．在区间[-1，5]上任取一个实数b，则曲线f（x）=x3-2x2+bx在点（1，f（1））处切线的倾斜角为钝角的概率为$\frac{1}{3}$．分析 利用曲线f（x）=x3-2x2+bx在点（1，f（1））处切线的倾斜角为钝角，求出b的范围，以长度为测度，即可求出所求概率．
解答 解：∵f（x）=x3-2x2+bx，
∴f′（x）=3x2-4x+b，
∴f′（1）=b-1＜0，∴b＜1．
由几何概型，可得所求概率为$\frac{1-（-1）}{5-（-1）}$=$\frac{1}{3}$．
故答案为$\frac{1}{3}$．
点评 本题考查概率的计算，考查导数的几何意义，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
19．已知集合A={x|x2+5x＞0}，B={x|-3＜x＜4}，则A∩B等于（ ）
| A． | （-5，0） | B． | （-3，0） | C． | （0，4） | D． | （-5，4） |
6．已知集合A={x|（x-2）（x+6）＞0}，B={x|-3＜x＜4}，则A∩B等于（ ）
| A． | （-3，-2） | B． | （-3，2） | C． | （2，4） | D． | （-2，4） |
3．执行如图所示的程序框图，若输出的结果是6，则判断框内m的取值范围是（ ）
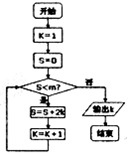
| A． | （30，42] | B． | （20，30） | C． | （20，30] | D． | （20，42） |
20．
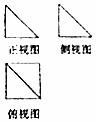如图是一个几何体的三视图，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，则该多面体的各条棱中最长棱的长度为（ ）
如图是一个几何体的三视图，其中正视图和侧视图是腰长为1的两个全等的等腰直角三角形，则该多面体的各条棱中最长棱的长度为（ ）| A． | $\sqrt{7}$ | B． | $\sqrt{5}$ | C． | 2 | D． | $\sqrt{3}$ |