题目内容
12.在某次数学考试中,考生的成绩ξ服从一个正态分布,即ξ~N(90,100).(1)试求考试成绩ξ位于区间(70,110)上的概率是多少?
(2)若这次考试共有2 000名考生,试估计考试成绩在(80,100)间的考生大约有多少人?
分析 (1)根据考生的成绩ξ~N(90,100),得到正态曲线关于x=90对称,根据3σ原则知P(70<x<110)=P(90-2×10<x<90+2×10)=0.9544;
(2)P(80<x<100)=P(90-10<x<90+10)=0.683,即可得到结果.
解答 解:(1)∵考生的成绩ξ服从正态分布,即ξ~N(90,100),
∴正态曲线关于x=90对称,且标准差为10,
根据3σ原则知P(70<x<110)=P(90-2×10<x<90+2×10)=0.9544,
(2)P(80<x<100)=P(90-10<x<90+10)=0.683,
考试成绩X位于区间(80,100)上的概率为0.683,
则估计考试成绩在(80,100)间的考生大约有2000×0.683=1366人.
点评 本题考查正态分布曲线的特点及曲线所表示的意义,解题的关键是注意利用正态曲线的对称性.

练习册系列答案
相关题目
2.某品牌汽车4S店对最近100位采用分期付款的购车者进行统计,统计结果如表所示:
已知分3期付款的频率为0.2,4S店经销一辆该品牌的汽车,顾客分1期付款,其利润为1万元;分2期或3期付款,其利润为1.5万元;分4期或5期付款,其利润为2万元,用Y表示经销一辆汽车的利润.
(1)求上表中a,b的值;
(2)若以频率作为概率,求事件A:“购买该品牌的3位顾客中,至多有一位采用分3期付款”的概率P(A);
(3)求Y的分布列及数学期望EY.
| 付款方式 | 分1期 | 分2期 | 分3期 | 分4期 | 分5期 |
| 频数 | 40 | 20 | a | 10 | b |
(1)求上表中a,b的值;
(2)若以频率作为概率,求事件A:“购买该品牌的3位顾客中,至多有一位采用分3期付款”的概率P(A);
(3)求Y的分布列及数学期望EY.
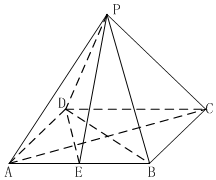 如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上E是AB的中点.
如图,四棱锥P-ABCD的底面ABCD为矩形,AB=2$\sqrt{2}$,BC=2,点P在底面上的射影在AC上E是AB的中点.