题目内容
设函数f(x)=x3-22-x的零点为x0,则x0所在的大致区间是( )
| A、(3,4) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
考点:函数零点的判定定理
专题:计算题,函数的性质及应用
分析:易知函数f(x)=x3-22-x在定义域上为连续增函数,从而由函数零点的判定定理确定区间.
解答:
解:易知函数f(x)=x3-22-x在定义域上为连续增函数,
又∵f(1)=1-2=-1<0,
f(2)=8-1=7>0;
故f(1)•f(2)<0;
故x0所在的大致区间是(1,2);
故选C.
又∵f(1)=1-2=-1<0,
f(2)=8-1=7>0;
故f(1)•f(2)<0;
故x0所在的大致区间是(1,2);
故选C.
点评:本题考查了函数零点的判定定理的应用,属于基础题.

练习册系列答案
相关题目
若x0是函数f(x)=(
)x-log3x的零点,且0<x1<x0,则f(x1)( )
| 1 |
| 5 |
| A、恒为正值 | B、等于0 |
| C、恒为负值 | D、不大于0 |
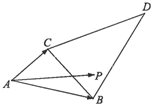
如图,△BCD与△ABC的面积之比为2,点P是区域ABCD内任意一点(含边界),且
=λ
+μ
(λ,μ∈R),则λ+μ的取值范围是( )
| AP |
| AB |
| AC |

| A、[0,1] |
| B、[0,2] |
| C、[0,3] |
| D、[0,4] |