题目内容
可以用集合语言将“公理1:如果直线l上有两个点在平面α上,那么直线l在平面α上.”表述为( )
| A、A?l,B?l且A?α,B?α,则l?α |
| B、若A∈l,B∈l且A∈α,B∈α,则l∈α |
| C、若A∈l,B∈l且A∈α,B∈α,则l?α |
| D、若A∈l,B∈l且A?α,B?α,则l∈α |
考点:平面的基本性质及推论
专题:空间位置关系与距离
分析:根据空间点线面关系的集合描述方法,将公理1中的点线面关系,转化为符号表示,即可得到答案.
解答:
解:在空间几何中,点可以看成是元素,线和面应看成是集合,
根据元素属于集合,子集包含于全集可得:
公理1:如果直线l上有两个点在平面α上,那么直线l在平面α上,用集合语言应表示为:
若A∈l,B∈l且A∈α,B∈α,则l?α,
故选:C
根据元素属于集合,子集包含于全集可得:
公理1:如果直线l上有两个点在平面α上,那么直线l在平面α上,用集合语言应表示为:
若A∈l,B∈l且A∈α,B∈α,则l?α,
故选:C
点评:本题考查的知识点是平面的基本性质及推论,其中会用符号语言准确的表述空间点,线,面之间的关系,是解答的关键.

练习册系列答案
相关题目
定义n!=1×2×…×n.如图是求10!的程序框图,则在判断框内应填的条件是( )


| A、i<10 | B、i>10 |
| C、i≤11 | D、i≤10 |
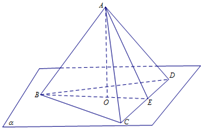 如图,正三棱锥A-BCD放置在平面α上,AD=kCD,O是底面△BCD的中心,E是CD的中点,下列说法中,错误的是( )
如图,正三棱锥A-BCD放置在平面α上,AD=kCD,O是底面△BCD的中心,E是CD的中点,下列说法中,错误的是( )A、k>
| ||||||||
B、当AD=CD=1时,将三棱锥绕直线AO旋转一周所形成的几何 体的体积是
| ||||||||
| C、动点P在截面ABE上运动,且到点B的距离与到点侧面ACD的距离相等,则点P在抛物线弧上 | ||||||||
D、当k=
|
角α的终边过点(2sin30°,-2cos30°),则cosα的值为( )
A、
| ||||
B、
| ||||
C、-
| ||||
D、-
|
在极坐标系中,曲线C1:ρ(
cosθ+sinθ)=1与曲线C2:ρ=a(a>0)的一个交点在极轴上,则a等于( )
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、2 |
已知集合M={y|y=x2-1},集合N={x|y=
},则∁RM∩N=( )
| 4-x2 |
| A、(-2,-1) |
| B、[-2,-1] |
| C、[-2,1) |
| D、[-2,-1) |
 由若干个棱长为1的正方体搭成的几何体主视图和俯视图相同(如图所示),现给出如下四个图形,可能为侧视图的个数为( )
由若干个棱长为1的正方体搭成的几何体主视图和俯视图相同(如图所示),现给出如下四个图形,可能为侧视图的个数为( )