题目内容
(1+
)6(1-
)4展开式中的常数项为 .
| 3 | x |
| 1 | ||
|
考点:二项式系数的性质
专题:二项式定理
分析:把二项式按照二项式定理展开,分析求得展开式中的常数项.
解答:
解:(1+
)6(1-
)4 =(
+
•x
+
•x
+…+
•x2)•(1-
•x-
+
•x-1-
•x-
+
•x-2),
故展开式中的常数项为 1+
•
+
•
=122,
故答案为:122.
| 3 | x |
| 1 | ||
|
| C | 0 6 |
| C | 1 6 |
| 1 |
| 3 |
| C | 2 6 |
| 2 |
| 3 |
| C | 6 6 |
| C | 1 4 |
| 1 |
| 2 |
| C | 2 4 |
| C | 3 4 |
| 3 |
| 2 |
| C | 4 4 |
故展开式中的常数项为 1+
| C | 3 6 |
| C | 2 4 |
| C | 6 6 |
| C | 4 4 |
故答案为:122.
点评:本题主要考查二项式定理的应用,二项式展开式的通项公式,求展开式中某项的系数,属于中档题.

练习册系列答案
相关题目
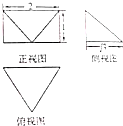
一个几何体的三视图如图所示,则该几何体的表面积为( )


A、
| ||||
B、9+4
| ||||
C、9+3
| ||||
D、
|
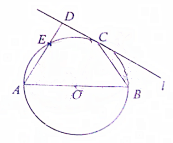 如图,圆O的直径AB=8,C为圆周上一点,BC=4,过C作圆的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E,则线段DE的长为
如图,圆O的直径AB=8,C为圆周上一点,BC=4,过C作圆的切线l,过A作直线l的垂线AD,D为垂足,AD与圆O交于点E,则线段DE的长为