题目内容
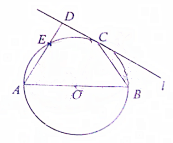如图，圆O的直径AB=8，C为圆周上一点，BC=4，过C作圆的切线l，过A作直线l的垂线AD，D为垂足，AD与圆O交于点E，则线段DE的长为考点：与圆有关的比例线段
专题：选作题,立体几何
分析：连接BE，OC，OC∩BE=F，证明四边形EFCD是矩形，△OBC是等边三角形，即可得出结论．
解答：
解：连接BE，OC，OC∩BE=F，则OC⊥l，
∵AD⊥l，
∴AD∥OC，
∵AB是圆O的直径，
∴AD⊥BE，
∵AD⊥l，
∴l∥BE，
∴四边形EFCD是矩形，
∴DE=CF，
∵圆O的直径AB=8，BC=4，
∴△OBC是等边三角形，
∴CF=2，
∴DE=2，
故答案为：2．
解：连接BE，OC，OC∩BE=F，则OC⊥l，∵AD⊥l，
∴AD∥OC，
∵AB是圆O的直径，
∴AD⊥BE，
∵AD⊥l，
∴l∥BE，
∴四边形EFCD是矩形，
∴DE=CF，
∵圆O的直径AB=8，BC=4，
∴△OBC是等边三角形，
∴CF=2，
∴DE=2，
故答案为：2．
点评：本题考查圆的切线的性质，考查学生的计算能力，属于中档题．
练习册系列答案
相关题目
已知公差不为零的等差数列{an}的首项是公差的4倍，若am是a1和a2m的等比例中项，则m=（ ）
| A、2 | B、3 | C、4 | D、5 |