题目内容
设直线l1：y=2x与直线l2：x+y=6交于P点．
（1）当直线m过P点且与直线l0：x-2y=0垂直时，求直线m的方程；
（2）当直线m过P点且坐标原点O到直线m的距离为2时，求直线m的方程．
（1）当直线m过P点且与直线l0：x-2y=0垂直时，求直线m的方程；
（2）当直线m过P点且坐标原点O到直线m的距离为2时，求直线m的方程．
考点：直线与圆锥曲线的综合问题
专题：综合题,直线与圆
分析：（1）先求出P的坐标，由直线m过P点且与直线l0：x-2y=0垂直时，可得直线m的斜率，从而可得直线m的方程；
（2）分类讨论，根据直线m过P点且坐标原点O到直线m的距离为2时，利用点到直线的距离公式，即可求出直线m的方程．
（2）分类讨论，根据直线m过P点且坐标原点O到直线m的距离为2时，利用点到直线的距离公式，即可求出直线m的方程．
解答：
解：（1）令2x=6-x，可得x=2，∴y=4，
∴交点（2 4）．
∵直线m和x-2y=0垂直，
∴直线m的斜率为-2，
∴直线m的方程y-4=-2（x-2），即2x+y-8=0；
（2）当直线的斜率存在时，设直线方程为y-4=k（x-2），即kx-y+4-2k=0
圆0到直线的距离d=
=2，
解得k=
，
∴直线m的方程为y-4=
（x-2），即3x-4y+10=0；
当直线的斜率不存在时，方程为x=2，符合题意，
综上，直线m的方程为x=2或3x-4y+10=0．
∴交点（2 4）．
∵直线m和x-2y=0垂直，
∴直线m的斜率为-2，
∴直线m的方程y-4=-2（x-2），即2x+y-8=0；
（2）当直线的斜率存在时，设直线方程为y-4=k（x-2），即kx-y+4-2k=0
圆0到直线的距离d=
| |-2k+4| | ||
|
解得k=
| 3 |
| 4 |
∴直线m的方程为y-4=
| 3 |
| 4 |
当直线的斜率不存在时，方程为x=2，符合题意，
综上，直线m的方程为x=2或3x-4y+10=0．
点评：本题考查直线方程，考查点到直线的距离公式，考查学生的计算能力，属于中档题．
练习册系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
已知函数f(x)=x+
，则函数y=f（x）的大致图象为（ ）
| ln|x| |
| x |
A、 |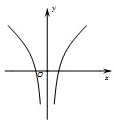
B、 |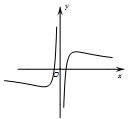
C、 |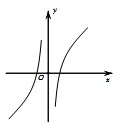
D、 |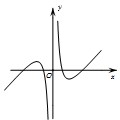
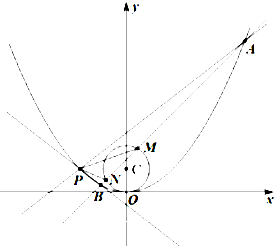设点P（-2，1）在抛物线x2=2py（p＞0）上，且到圆C：x2+（y+b）2=1上点的最小距离为1．