题目内容
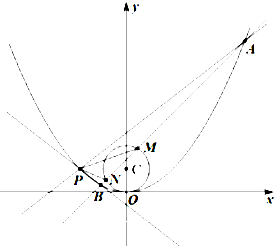 设点P(-2,1)在抛物线x2=2py(p>0)上,且到圆C:x2+(y+b)2=1上点的最小距离为1.
设点P(-2,1)在抛物线x2=2py(p>0)上,且到圆C:x2+(y+b)2=1上点的最小距离为1.(Ⅰ)求p和b的值;
(Ⅱ)过点P作两条斜率互为相反数的直线,分别与抛物线交于两点A,B,若直线AB与圆C交于不同两点M,N.
(i)证明直线AB的斜率为定值;
(ii)求△PMN面积取最大值时直线AB的方程.
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(Ⅰ)由点P(-2,1)在抛物线x2=2py(p>0)上,能求出p,由已知条件利用两点间距离公式能求出b.
(Ⅱ)(i)设直线PA的斜率为k,则直线PB的斜率为-k,联立
,推导出A(4k+2,(2k+1)2),B(-4k+2,(-2k+1)2),由此能求出直线AB的斜率.
(ii)设直线AB的方程为y=x+t,联立直线AB与圆C的方程,得2x2+2(t-1)x+t2-2t=0,利用导数知识能求出△PMN面积取最大值时直线AB的方程
(Ⅱ)(i)设直线PA的斜率为k,则直线PB的斜率为-k,联立
|
(ii)设直线AB的方程为y=x+t,联立直线AB与圆C的方程,得2x2+2(t-1)x+t2-2t=0,利用导数知识能求出△PMN面积取最大值时直线AB的方程
解答:
(Ⅰ)解:∵点P(-2,1)在抛物线x2=2py(p>0)上,
∴(-2)2=2p,解得p=2,
∵点P(-2,1)到圆C:x2+(y+b)2=1上点的最小距离为1,
∴
=1+1,解得b=-1.
(Ⅱ)(i)证明:设直线PA的斜率为k,则直线PB的斜率为-k,
∴直线PA的方程为y-1=k(x+2),
联立
,
整理,得x2-4kx-8k-4=0,
根据韦达定理,有xA+xP=4k,
∴xA=4k+2,∴A(4k+2,(2k+1)2),
同理B(-4k+2,(-2k+1)2),
∴直线AB的斜率为:kAB=
=1.
(ii)设直线AB的方程为y=x+t,则点P到直线AB的距离d=
,
联立直线AB与圆C的方程,得
,
整理,得2x2+2(t-1)x+t2-2t=0,
∵AB与圆C交于不同两点M,N,∴1-
<t<1+
,
∵|MN|=
•
=
•
,
∴S△PMN=
•
•
•
=
,(1-
<t<<1+
),
设m=(t-3)2•(-t2+2t+1),
∵m′=2(t-3)•(-t2+2t+1)+(t-3)2•(-2t+2),
由m′=0,解得t=
,或t=
(舍),或t=3(舍),
∴(S△PMN)max=
•
,
此时直线AB的方程为y=x+
.
∴(-2)2=2p,解得p=2,
∵点P(-2,1)到圆C:x2+(y+b)2=1上点的最小距离为1,
∴
| (-2-0)2+(1+b)2 |
(Ⅱ)(i)证明:设直线PA的斜率为k,则直线PB的斜率为-k,
∴直线PA的方程为y-1=k(x+2),
联立
|
整理,得x2-4kx-8k-4=0,
根据韦达定理,有xA+xP=4k,
∴xA=4k+2,∴A(4k+2,(2k+1)2),
同理B(-4k+2,(-2k+1)2),
∴直线AB的斜率为:kAB=
| (2k+1)2-(-2k+1)2 |
| 4k+2-(-4k+2) |
(ii)设直线AB的方程为y=x+t,则点P到直线AB的距离d=
| |t-3| | ||
|
联立直线AB与圆C的方程,得
|
整理,得2x2+2(t-1)x+t2-2t=0,
∵AB与圆C交于不同两点M,N,∴1-
| 2 |
| 2 |
∵|MN|=
| 2 |
| ||
| 2 |
=
| 2 |
| -t2+2t+1 |
∴S△PMN=
| 1 |
| 2 |
| |t-3| | ||
|
| 2 |
| -t2+2t+1 |
=
| 1 |
| 2 |
| (t-3)2•(-t2+2t+1 |
| 2 |
| 2 |
设m=(t-3)2•(-t2+2t+1),
∵m′=2(t-3)•(-t2+2t+1)+(t-3)2•(-2t+2),
由m′=0,解得t=
3-
| ||
| 2 |
3+
| ||
| 2 |
∴(S△PMN)max=
3+
| ||
| 4 |
|
此时直线AB的方程为y=x+
3-
| ||
| 2 |
点评:本题考查圆锥曲线中参数的求法,考查直线斜率为定理的证明,考查三角形面积最大时直线方程的求法.

练习册系列答案
 互动英语系列答案
互动英语系列答案 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案
相关题目
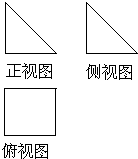 一几何体的三视图如图所示,若正视图和侧视图都是等腰直角三角形,直角边长为1,则该几何体外接球的表面积为( )
一几何体的三视图如图所示,若正视图和侧视图都是等腰直角三角形,直角边长为1,则该几何体外接球的表面积为( )A、
| ||
| B、2π | ||
| C、3π | ||
| D、12π |
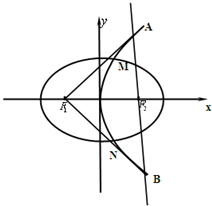 已知椭圆C的焦点为F1(-1,0)、F2(1,0),点P(-1,
已知椭圆C的焦点为F1(-1,0)、F2(1,0),点P(-1,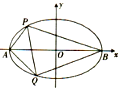 如图,以
如图,以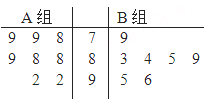 天府新区的战略定位是以城乡一体化、全面现代化、充分引进国际化为引领,并以现代制造业为主,高端服务业集聚,宜业宜商宜居的国际化现代新城区,为引进优秀厂家,某企业对16家厂家根据地域分为两组,分别由A、B两组评委对各项指标进行综合评比打分,两个组队对16家厂家评比最后综合得分的茎叶图如图所示,其中茎为十位数,叶为个位数,若某厂家总和得分高于16家厂家的平均分则确定为优秀厂家.
天府新区的战略定位是以城乡一体化、全面现代化、充分引进国际化为引领,并以现代制造业为主,高端服务业集聚,宜业宜商宜居的国际化现代新城区,为引进优秀厂家,某企业对16家厂家根据地域分为两组,分别由A、B两组评委对各项指标进行综合评比打分,两个组队对16家厂家评比最后综合得分的茎叶图如图所示,其中茎为十位数,叶为个位数,若某厂家总和得分高于16家厂家的平均分则确定为优秀厂家.