题目内容
10.已知100件产品中有4件次品,无放回地从中抽取2次,每次抽取1件,求下列事件的概率:(1)第一次取到次品,第二次取到正品;
(2)两次都取到正品;
(3)两次抽取中恰有一次取到正品.
分析 分别确定基本事件的总数,满足条件的基本事件数,即可求出概率.
解答 解:(1)设第一取得次品的事件为A,第二次取得正品的事件为B,
∴P=P(A)•P(B)=$\frac{4}{100}•\frac{96}{99}$=$\frac{32}{825}$=0.388;
(2)P=$\frac{96}{100}•\frac{95}{99}$=$\frac{152}{165}$=0.912;
(3)P=$\frac{96}{100}•\frac{4}{99}+\frac{4}{100}•\frac{96}{99}$=$\frac{64}{825}$=0.0776.
点评 本题考查概率的计算,考查学生分析解决问题的能力,确定基本事件数是关键,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载新产品A、B若干件,该所要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排,通过调查,有关数据如表:
并且B产品的数量不超过A产品数量的2倍.如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
| 每件产品A | 每件产品B | ||
| 研制成本、搭载费用之和(百万元) | 2 | 1.5 | 计划最大资金额15(百万元) |
| 产品重量(千克) | 1 | 1.5 | 最大搭载重量12(千克) |
| 预计收益(百元) | 1000 | 1200 | 10200(百元) |
5.一个盒子里装有相同大小的黑球10个,红球12个,白球4个,从中任取2个,其中白球为X,则下列算式中等于$\frac{{C}_{22}^{1}{C}_{4}^{1}+{C}_{22}^{2}}{{C}_{26}^{2}}$的是( )
| A. | P(0<X≤2) | B. | P(X≤1) | C. | P(X=1) | D. | P(X=2) |
19.平面四边形ABCD中,根据向量关系( ),可推知其为平行四边形.
| A. | $\overrightarrow{AB}$=2$\overrightarrow{DC}$ | B. | $\overrightarrow{AB}$=-$\overrightarrow{CD}$ | C. | |$\overrightarrow{AB}$|=|$\overrightarrow{DC}$| | D. | |$\overrightarrow{AB}$|=|$\overrightarrow{BC}$| |
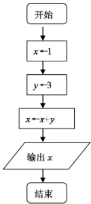 如图所示的算法语句中,输出的结果是x=4.
如图所示的算法语句中,输出的结果是x=4.