题目内容
9.若将函数f(x)=sin2x+cos2x的图象向右平移φ(φ>0)个单位,所得图象关于原点对称,则φ的最小值为( )| A. | $\frac{π}{8}$ | B. | $\frac{π}{4}$ | C. | $\frac{3π}{8}$ | D. | $\frac{3π}{4}$ |
分析 把函数式f(x)=sin2x+cos2x化积为f(x)=$\sqrt{2}$sin(2x+$\frac{π}{4}$),然后利用三角函数的图象平移得到y=$\sqrt{2}$sin(2x+$\frac{π}{4}$-2φ).结合该函数为偶函数求得φ的最小正值.
解答 解:∵由f(x)=sin2x+cos2x=$\sqrt{2}$sin(2x+$\frac{π}{4}$),
∴把该函数的图象右移φ个单位,所得图象对应的函数解析式为:y=$\sqrt{2}$sin[2(x-φ)+$\frac{π}{4}$]=$\sqrt{2}$sin(2x+$\frac{π}{4}$-2φ).
∵所得图象关于原点对称,则$\frac{π}{4}$-2φ=kπ,k∈Z.
∴当k=0时,φ有最小正值是$\frac{π}{8}$.
故选:A.
点评 本题考查了三角函数的图象平移,考查了三角函数奇偶性的性质,是中档题.

练习册系列答案
相关题目
1.某研究所计划利用“神七”宇宙飞船进行新产品搭载实验,计划搭载新产品A、B若干件,该所要根据该产品的研制成本、产品重量、搭载实验费用和预计产生收益来决定具体安排,通过调查,有关数据如表:
并且B产品的数量不超过A产品数量的2倍.如何安排这两种产品的件数进行搭载,才能使总预计收益达到最大,最大收益是多少?
| 每件产品A | 每件产品B | ||
| 研制成本、搭载费用之和(百万元) | 2 | 1.5 | 计划最大资金额15(百万元) |
| 产品重量(千克) | 1 | 1.5 | 最大搭载重量12(千克) |
| 预计收益(百元) | 1000 | 1200 | 10200(百元) |
19.平面四边形ABCD中,根据向量关系( ),可推知其为平行四边形.
| A. | $\overrightarrow{AB}$=2$\overrightarrow{DC}$ | B. | $\overrightarrow{AB}$=-$\overrightarrow{CD}$ | C. | |$\overrightarrow{AB}$|=|$\overrightarrow{DC}$| | D. | |$\overrightarrow{AB}$|=|$\overrightarrow{BC}$| |
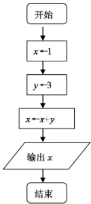 如图所示的算法语句中,输出的结果是x=4.
如图所示的算法语句中,输出的结果是x=4.