题目内容
（1）方程2x3-6x2+3=0有几个解？如果有解，全部解的和为多少？
（2）探究方程2x3-6x2+5=0，2x3-6x2+8=0的全部解的和，你由此可以得出什么结论？
（2）探究方程2x3-6x2+5=0，2x3-6x2+8=0的全部解的和，你由此可以得出什么结论？
考点：函数的零点
专题：计算题,函数的性质及应用,推理和证明
分析：（1）设函数f（x）=2x3-6x2+3，利用二分法求方程2x3-6x2+3=0的解的个数及近似解，从而确定和；
（2）利用二分法再求方程2x3-6x2+5=0，2x3-6x2+8=0的全部解的和，从而由归纳推理得到结论．
（2）利用二分法再求方程2x3-6x2+5=0，2x3-6x2+8=0的全部解的和，从而由归纳推理得到结论．
解答：
解：（1）设函数f（x）=2x3-6x2+3，
∵f（-1）=-5＜0，f（0）=3＞0，f（1）=-1＜0，f（2）=-5＜0，f（3）=3＞0；
又∵函数f（x）=2x3-6x2+3的图象是连续的曲线；
∴方程2x3-6x2+3=0有三个实数解．
∵f（-1）•f（0）＜0，
∴在区间（-1，0）内有一个解． 取区间（-1，0）的中点x1=-0.5，
用计算器可算得f（-0.5）=1.25＞0．
∵f（-1）•f（-0.5）＜0，
∴x0∈（-1，-0.5）．
依次可得
x0∈（-0.75，-0.5），x0∈（-0.75，-0.625），x0∈（-0.687 5，-0.625），x0∈（-0.656 25，-0.625），
x0∈（-0.656 25，-0.640 625），x0∈（-0.648 437 5，-0.640 625），x0∈（-0.644 531 25，-0.640 625）．
由于|（-0.640 625）-（-0.644 531 25）|＜0.01，
此时区间（-0.644 531 25，-0.640 625）的两个端点精确到0.01的近似值都是-0.64，
所以方程2x3-6x2+3=0在区间（-1，0）且精确到0.01的近似解约为-0.64．
同理可求得方程2x3-6x2+3=0在区间（0，1）和（2，3）内且精确到0.01的近似解分别为 0.83，2.81．
所以，方程2x3-6x2+3=0的三个解的和为-0.64+0.83+2.81=3．
（2）利用同样的方法可求得方程2x3-6x2+5=0和2x3-6x2+8=0的所有解的和也为3．
故由此可归纳出结论：
一般地，对于一元三次方程ax3+bx2+d=0有三个根x1，x2，x3，则x1+x2+x3=-
．
∵f（-1）=-5＜0，f（0）=3＞0，f（1）=-1＜0，f（2）=-5＜0，f（3）=3＞0；
又∵函数f（x）=2x3-6x2+3的图象是连续的曲线；
∴方程2x3-6x2+3=0有三个实数解．
∵f（-1）•f（0）＜0，
∴在区间（-1，0）内有一个解． 取区间（-1，0）的中点x1=-0.5，
用计算器可算得f（-0.5）=1.25＞0．
∵f（-1）•f（-0.5）＜0，
∴x0∈（-1，-0.5）．
依次可得
x0∈（-0.75，-0.5），x0∈（-0.75，-0.625），x0∈（-0.687 5，-0.625），x0∈（-0.656 25，-0.625），
x0∈（-0.656 25，-0.640 625），x0∈（-0.648 437 5，-0.640 625），x0∈（-0.644 531 25，-0.640 625）．
由于|（-0.640 625）-（-0.644 531 25）|＜0.01，
此时区间（-0.644 531 25，-0.640 625）的两个端点精确到0.01的近似值都是-0.64，
所以方程2x3-6x2+3=0在区间（-1，0）且精确到0.01的近似解约为-0.64．
同理可求得方程2x3-6x2+3=0在区间（0，1）和（2，3）内且精确到0.01的近似解分别为 0.83，2.81．
所以，方程2x3-6x2+3=0的三个解的和为-0.64+0.83+2.81=3．
（2）利用同样的方法可求得方程2x3-6x2+5=0和2x3-6x2+8=0的所有解的和也为3．
故由此可归纳出结论：
一般地，对于一元三次方程ax3+bx2+d=0有三个根x1，x2，x3，则x1+x2+x3=-
| b |
| a |
点评：本题考查了二分法的应用及归纳推理的应用，属于基础题．
练习册系列答案
相关题目
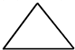
若一个正四棱锥的左视图是一个边长为2的正三角形（如图），则该正四棱锥的体积是（ ）
| A、1 | ||||
B、
| ||||
C、
| ||||
D、2
|
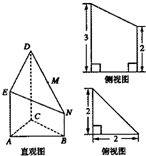如图是某几何体的直观图与三视图的侧视图、俯视图．在直观图中，2BN=AE，M是ND的中点．侧视图是直角梯形，俯视图是等腰直角三角形，有关数据如图所示．