��Ŀ����
9������y=sin ��2x+$\frac{��}{3}$����ͼ����ɺ���y=cosx��ͼ������| A�� | �ȰѸ���ĺ��������̵�ԭ����$\frac{1}{2}$����������ƽ��$\frac{��}{6}$����λ | |
| B�� | �ȰѸ���ĺ��������̵�ԭ����$\frac{1}{2}$����������ƽ��$\frac{��}{12}$����λ | |
| C�� | �ȰѸ���ĺ������쳤��ԭ����2����������ƽ��$\frac{��}{6}$����λ | |
| D�� | �ȰѸ���ĺ������쳤��ԭ����2����������ƽ��$\frac{��}{12}$����λ |
���� �����յ���ʽ��y=Asin����x+�գ���ͼ��任���ɣ��ó����ۣ�
��� �⣺�Ѻ���y=cosx=sin��x+$\frac{��}{2}$����ͼ��ĺ������Ϊԭ����$\frac{1}{2}$�����ɵ�y=sin��2x+$\frac{��}{2}$����ͼ��
�ٰ�����ͼ��������ƽ��$\frac{��}{12}$����λ���ɵ�y=sin[2��x-$\frac{��}{12}$��+$\frac{��}{2}$]=sin��2x+$\frac{��}{3}$����ͼ��
��ѡ��B��
���� ������Ҫ�����յ���ʽ��y=Asin����x+�գ���ͼ��任���ɣ����ڻ����⣮

��ϰ��ϵ�д�
 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
�����Ŀ
17�����к����У�ͼ���һ��������ͼ��ʾ���ǣ�������
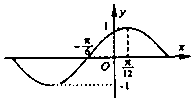

| A�� | $y=sin��{x+\frac{��}{6}}��$ | B�� | $y=cos��{2x-\frac{��}{6}}��$ | C�� | $y=sin��{2x-\frac{��}{6}}��$ | D�� | $y=cos��{4x-\frac{��}{3}}��$ |
1��ij�����������ͼ��ͼ��ʾ����ü����������ǣ�������
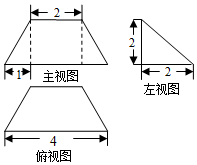

| A�� | 4 | B�� | $\frac{16}{3}$ | C�� | $\frac{20}{3}$ | D�� | 12 |
19����֪����f��x��=$\left\{\begin{array}{l}��3a-2��x+6a-1��x��1��\\{a^x}��x��1��\end{array}\right.$�����ݼ�����ôʵ��a��ȡֵ��Χ�ǣ�������
| A�� | ��0��1�� | B�� | ��0��$\frac{2}{3}$�� | C�� | [$\frac{3}{8}$��$\frac{2}{3}$�� | D�� | [$\frac{3}{8}$��1�� |
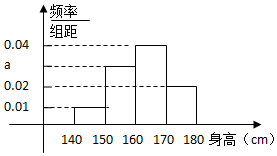 ij��ѧ�Ը����꼶��������ͳ�ƣ����������ȡ��20��ѧ�������ߣ���Ƶ�ʷֲ�ֱ��ͼ��ͼ����λ��cm��
ij��ѧ�Ը����꼶��������ͳ�ƣ����������ȡ��20��ѧ�������ߣ���Ƶ�ʷֲ�ֱ��ͼ��ͼ����λ��cm�� ��ͼ����֪б������ABC-A1B1C1�������ⳤ��Ϊ2����B1BA=$\frac{��}{3}$��M��N�ֱ�ΪA1C1��B1C���е㣬�Ҳ���ABB1A1�͵���ABC��
��ͼ����֪б������ABC-A1B1C1�������ⳤ��Ϊ2����B1BA=$\frac{��}{3}$��M��N�ֱ�ΪA1C1��B1C���е㣬�Ҳ���ABB1A1�͵���ABC��