题目内容
14. 如图,已知斜三棱柱ABC-A1B1C1的所有棱长均为2,∠B1BA=$\frac{π}{3}$,M,N分别为A1C1与B1C的中点,且侧面ABB1A1⊥底面ABC.
如图,已知斜三棱柱ABC-A1B1C1的所有棱长均为2,∠B1BA=$\frac{π}{3}$,M,N分别为A1C1与B1C的中点,且侧面ABB1A1⊥底面ABC.(Ⅰ)证明:MN∥平面ABB1A1
(Ⅱ)求三棱柱B1-ABC的体积.
分析 (Ⅰ)取AC中点P,连结PN,PM,从而PN∥AB1,PM∥AA1,从而平面PMN∥平面AB1A1,由此能证明MN∥平面ABB1A1.
(Ⅱ)连结PB,过B1作BO⊥平面ABC,推导出O是AB中点,由此能求出三棱柱B1-ABC的体积.
解答 证明:(Ⅰ)取AC中点P,连结PN,PM,
∵斜三棱柱ABC-A1B1C1中,M,N分别为A1C1与B1C的中点,
∴PN∥AB1,PM∥AA1,
∵PM∩PN=P,AB1∩AA=A,
PM,PN?平面PMN,AB1,AA1?平面AB1A1,
∴平面PMN∥平面AB1A1,
∵MN?平面PMN,∴MN∥平面ABB1A1.
解:(Ⅱ)连结PB,过B1作BO⊥平面ABC,
∵斜三棱柱ABC-A1B1C1的所有棱长均为2,∠B1BA=$\frac{π}{3}$,
M,N分别为A1C1与B1C的中点,且侧面ABB1A1⊥底面ABC.
∴△ABB1是边长为2的等边三角形,∴O是AB中点,∴B1O=$\sqrt{4-1}=\sqrt{3}$,
∵${S}_{△ABC}=\frac{1}{2}×2×2×sin60°$=$\sqrt{3}$,
∴三棱柱B1-ABC的体积V=$\frac{1}{3}×{S}_{△ABC}×{B}_{1}O$=$\frac{1}{3}×\sqrt{3}×\sqrt{3}$=1.
点评 本题考查线面平行的证明,考查三棱柱的体积的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
5.下列说法中正确的是( )
| A. | 一个命题的逆命题为真,则它的逆否命题一定为真 | |
| B. | “|a|>|b|”与“a2>b2”不等价. | |
| C. | “a2+b2=0,则a,b全为0”的逆否命题是“若a,b全不为0,则a2+b2≠0”. | |
| D. | 一个命题的否命题为真,则它的逆命题一定为真. |
9.函数y=sin (2x+$\frac{π}{3}$)的图象可由函数y=cosx的图象( )
| A. | 先把各点的横坐标缩短到原来的$\frac{1}{2}$倍,再向左平移$\frac{π}{6}$个单位 | |
| B. | 先把各点的横坐标缩短到原来的$\frac{1}{2}$倍,再向右平移$\frac{π}{12}$个单位 | |
| C. | 先把各点的横坐标伸长到原来的2倍,再向左平移$\frac{π}{6}$个单位 | |
| D. | 先把各点的横坐标伸长到原来的2倍,再向右平移$\frac{π}{12}$个单位 |
6.已知正方体ABCD-A1B1C1D1,平面α过直线BD,α⊥平面AB1C,α∩平面AB1C=m,平面β过直线A1C1,β∥平面AB1C,β∩平面ADD1A1=n,则m,n所成角的余弦值为( )
| A. | 0 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{2}}}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
4.已知m=$\frac{tan(α+β+γ)}{tan(α-β+γ)}$,若sin2(α+γ)=3sin2β,则m=( )
| A. | -1 | B. | $\frac{3}{4}$ | C. | $\frac{3}{2}$ | D. | 2 |
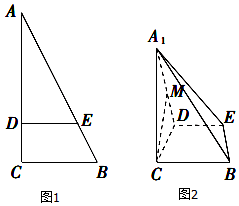 如图,在△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2.将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD.
如图,在△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2.将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD.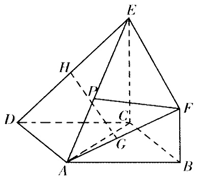 在如图所示的空间几何体中,EC⊥平面ABCD,四边形ABCD是菱形,CE∥BF,且CE=2BF,G,H,P分别为AF,DE,AE的中点.求证:
在如图所示的空间几何体中,EC⊥平面ABCD,四边形ABCD是菱形,CE∥BF,且CE=2BF,G,H,P分别为AF,DE,AE的中点.求证: 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(2,$\sqrt{2}$),离心率e=$\frac{\sqrt{2}}{2}$,直线l的渐近线为x=4.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)经过点P(2,$\sqrt{2}$),离心率e=$\frac{\sqrt{2}}{2}$,直线l的渐近线为x=4.