题目内容
20.设命题p:?x∈R,x2-ax+1≥0,命题q:?x>0,$\frac{{x}^{2}+1}{x}$<a,若(¬p)∨q是真命题,求实数a的取值范围.分析 解法一:由(?p)∨q是真命题,得以下三种情况:(1)?p与q都是真命题,(2)?p是真命题,q是假命题,(3)?p是假命题,q是真命题,进而得到实数a的取值范围.
解法二:由(?p)∨q是真命题,即 (?p)或q至少一个真,进而得到实数a的取值范围.
解答 (本题满分10分)
解:若p真,则有△=a2-4≤0,…(2分)
即-2≤a≤2,.…(3分)
∴?P:a>2或a<-2,…(4分)
若q真,由$\frac{{{x^2}+1}}{x}=x+\frac{1}{x}≥2$,…(5分)
得a>2.…(6分)
解法一:由(?p)∨q是真命题,得以下三种情况:
(1)?p与q都是真命题,这时符合条件的实数a>2;…(7分)
(2)?p是真命题,q是假命题,这时有a<-2;…(8分)
(3)?p是假命题,q是真命题,这时不存在符合条件的实数a.…(9分)
综上所述,实数a的取值范围是(-∞,-2)∪(2,+∞).…(10分)
解法二:由(?p)∨q是真命题,即 (?p)或q至少一个真…(7分)
由 a>2或a<-2和 a>2取并集 …(8分)
得实数a的取值范围是 (-∞,-2)∪(2,+∞)…(10分)
注:其他解法请参照给分.
点评 本题以命题的真假判断与应用为载体,考查了复合命题,特称命题,全称命题等知识点,难度中档.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
15.已知m>e>n>1>k>0(e为自然数2.7…),且x=m${\;}^{\frac{1}{e}}$,y=lnn,z=logke,则( )
| A. | x>y>z | B. | x>z>y | C. | y>x>z | D. | y>z>x |
5.已知集合M={x|(x+2)(x-3)≤0},N={-3,-1,1,3,5},则M∩N=( )
| A. | {1,3} | B. | {-3,-1,1} | C. | {-3,1} | D. | {-1,1,3} |
10.若偶函数f(x)在[1,+∞)上是减函数,则下列关系式中成立的是( )
| A. | $f(2)<f(-\frac{3}{2})<f(-1)$ | B. | $f(-\frac{3}{2})<f(-1)<f(2)$ | C. | $f(2)<f(-1)<f(-\frac{3}{2})$ | D. | $f(-1)<f(-\frac{3}{2})<f(2)$ |
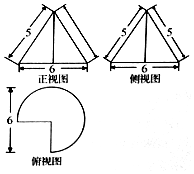 一个几何体的三视图如图所示,正视图和侧视图是两个全等的三角形,俯视图是$\frac{3}{4}$个圆,则该几何体的体积等于9π.
一个几何体的三视图如图所示,正视图和侧视图是两个全等的三角形,俯视图是$\frac{3}{4}$个圆,则该几何体的体积等于9π.