Question

5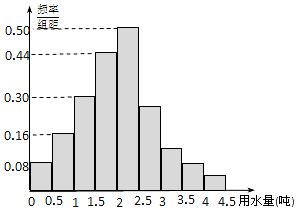．某地区100位居民的人均月用水量（单位：t）的频率分布直方图及频数分布表如下：

分组	频数
[0，0.5）	4
[0.5，1）	8
[1，1.5）	15
[1.5，2）	22
[2，2.5）	25
[2.5，3）	14
[3，3.5）	6
[3.5，4）	4
[4，4.5）	2
合计	100

（1）根据频率分布直方图估计这组数据的众数与平均数；
（2）当地政府制定了人均月用水量为3t的标准，若超出标准加倍收费，当地政府解释说，85%以上的居民不超出这个标准，这个解释对吗？为什么？

Answer 1

分析 （1）频率最大的组的组中值，即为众数，累加各组组中与频率的乘积，可得平均数；
（2）累加月均用水量在3t以上的频率，进而得到月均用水量在3t以下的频率，可得结合．

解答 解：（1）由图知，这组数据的众数为2.25，
平均数
为0.25×0.04+0.75×0.08+1.25×0.15+1.75×0.22+2.25×0.25+2.75×0.14+3.25×0.06+3.75×0.04+4.25×0.02=2.02；
（2）人均月用水量在3t以上的居民的比例为6%+4%+2%=12%，
即大约是有12%的居民月均用水量在3t以上，
88%的居民月均用水量在3t以下，
因此，政府的解释是正确的．

点评 本题考查的知识点是频率分布直方图，频率分布直方表，难度不大，属于基础题．