题目内容
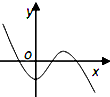
已知f(x)是二次函数,不等式f(x)<0的解集为(0,5),且在区间[-1,4]上的最大值为12.
(1)求f(x)的解析式;
(2)解关于x的不等式:
>1(m>0).
(1)求f(x)的解析式;
(2)解关于x的不等式:
| 2x2+(m-10)x-m2 |
| f(x) |
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)由题意可设f(x)=ax(x-5),a>0.再根据在区间[-1,4]上的最大值为f(-1)=12,求得a的值,可得f(x)的解析式.
(2)关于x的不等式即
>1,即2mx(x-m)(x-5)>0,分类讨论求得它的解集.
(2)关于x的不等式即
| 2x2+(m-10)x-m2 |
| 2x2-10x |
解答:
解:(1)由题意可得,可设f(x)=ax(x-5),a>0.
再根据在区间[-1,4]上的最大值为f(-1)=6a=12,求得 a=2,可得f(x)=2x(x-5)=2x2-10x.
(2)关于x的不等式:
>1(m>0),即
>1,
即
>0,即 2mx(x-m)(x-5)>0.
当0<m<5时,求得它的解集为(0,m)∪(5,+∞);
当m≥5时,求得它的解集为(0,5)∪(m,+∞).
再根据在区间[-1,4]上的最大值为f(-1)=6a=12,求得 a=2,可得f(x)=2x(x-5)=2x2-10x.
(2)关于x的不等式:
| 2x2+(m-10)x-m2 |
| f(x) |
| 2x2+(m-10)x-m2 |
| 2x2-10x |
即
| mx-m2 |
| 2x2-10x |
当0<m<5时,求得它的解集为(0,m)∪(5,+∞);
当m≥5时,求得它的解集为(0,5)∪(m,+∞).
点评:本题主要考查二次函数的性质,分式不等式的解法,体现了转化、分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目


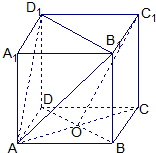 已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.
已知正方体ABCD-A1B1C1D1,O是底ABCD对角线的交点.