Question

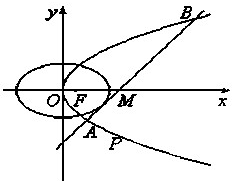如图所示，已知椭圆C₁和抛物线C₂有公共焦点F（1，0），C₁的中心和C₂的顶点都在坐标原点，过点M（4，0）的直线l与抛物线C₂分别相交于A，B两点．
（Ⅰ）写出抛物线C₂的标准方程；
（Ⅱ）求证：以AB为直径的圆过原点；
（Ⅲ）若坐标原点关于直线l的对称点P在抛物线C₂上，直线l与椭圆C₁相切，求椭圆C₁的标准方程．

Answer 1

考点：直线与圆锥曲线的综合问题

专题：综合题,圆锥曲线的定义、性质与方程

分析：（Ⅰ）设出抛物线C₂的标准方程，利用焦点F（1，0），即可得出结论；
（Ⅱ）设AB：x=4+ny，代入抛物线方程，证明

OA

•

OB

=0，即可得出结论；
（Ⅲ）P（4t²，4t），则OP⊥l，且OP的中点（2t²，2t）在直线l上，直线方程代入椭圆方程，利用△=0，可得结论．

解答： （Ⅰ）解：抛物线C₂的标准方程为：y²=2px，
∵焦点F（1，0），
∴p=2
∴抛物线C₂的标准方程为y²=4x；
（Ⅱ）证明：设AB：x=4+ny，代入抛物线方程得y²-4ny-16=0，
设A（x₁，y₁），B（x₂，y₂），则y₁y₂=-16，x₁x₂=

y12y22

16

=16，
∴

OA

•

OB

=x₁x₂+y₁y₂=0，
∴以AB为直径的圆过原点；
（Ⅲ）解：设P（4t²，4t），则OP⊥l，且OP的中点（2t²，2t）在直线l上，
∴

2t2=4+2nt 4t 4t2 =-n

，∴n=±1，
由

b2x2+a2y2=a2b2 x=4+ny

，得（b²n²+a²）y²+8b²ny+b²（16-a²）=0，
由△=0，可得a²+b²=16，
∵a²=b²+1，
∴a2=

17

2

，b2=

15

2

，
∴椭圆C₁的标准方程为

2x2

17

+

2y2

15

=1．

点评：本题考查抛物线的标准方程，考查直线与抛物线的位置关系，考查直线与椭圆的位置关系，考查学生分析解决问题的能力，属于中档题．