��Ŀ����
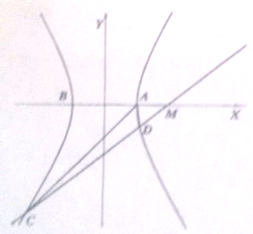 ��ͼ��ʾ����֪˫����
��ͼ��ʾ����֪˫����| x2 |
| a2 |
| y2 |
| b2 |
��1����a=2��b=
| 3 |
��2����x�����Ƿ��������һ������M���ˣ�0������M��ֱ����˫��������������C��D������������ô��תֱ��CD���ڱ�ֱ֤�ߺ�˫���������������ǰ���£���ʼ��CA��AD��������ڣ�������˵�ֵ����������ڣ���˵�����ɣ�
���㣺ֱ����Բ���ߵ��ۺ�����
ר�⣺Բ�����е���ֵ�뷶Χ����
��������1�������������Ƶ���˫���߷���Ϊ
-
=1������
���ã�x2-32x+76=0��������Բ�ҳ���ʽ������߶�CD�ij��ȣ�
��2��������ڶ���M���ˣ�0������M��ֱ����˫��������������C��D������������ô��תֱ��CD��ʼ��CA��AD����ֱ��CD�ķ���Ϊy=k��x-�ˣ�����C��x3��y3����D��x4��y4������A��2��0�����ֱ����CA��AD��б�ʣ���CA��AD���õ�CA��AD��ֱ�ߵ�бб�ʵij˻�Ϊ-1���ɴ˵õ�һ������ʽ���ٰѵ�C��D������ֱ����ֱ��CD�ķ��̵õ���һ������ʽ���Ƚ���������ʽ����������
| x2 |
| 4 |
| y2 |
| 3 |
|
��2��������ڶ���M���ˣ�0������M��ֱ����˫��������������C��D������������ô��תֱ��CD��ʼ��CA��AD����ֱ��CD�ķ���Ϊy=k��x-�ˣ�����C��x3��y3����D��x4��y4������A��2��0�����ֱ����CA��AD��б�ʣ���CA��AD���õ�CA��AD��ֱ�ߵ�бб�ʵij˻�Ϊ-1���ɴ˵õ�һ������ʽ���ٰѵ�C��D������ֱ����ֱ��CD�ķ��̵õ���һ������ʽ���Ƚ���������ʽ����������
���
�⣺��1����˫����
-
=1��a=2��b=
��
��˫���߷���Ϊ
-
=1��
����
����ȥy�����������ã�x2-32x+76=0��
��C��x1��y1����D��x2��y2������x1+x2=32��x1x2=76��
��|CD|=
=12
��
���߶�CD�ij���Ϊ12
��
��2��������ڶ���M���ˣ�0������M��ֱ����˫��������������C��D��
����������ô��תֱ��CD��ʼ��CA��AD��
��ֱ��CD�ķ���Ϊy=k��x-�ˣ���
��C��x3��y3����D��x4��y4����
��A��2��0������kCA=
��kAD=
��
��CA��AD����kCA•kAD=
•
=-1��
��������y3y4=-x3x4+2��x3+x4��-4����
��y=k��x-�ˣ���
��y3y4=[k��x3-�ˣ�][k��x4-�ˣ�]
=k2x3x4-k2�ˣ�x3+x4��+k2��2����
�ɢ٢ڣ���k2=-1����=2����������
����������Ķ���M���ˣ�0����
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
��˫���߷���Ϊ
| x2 |
| 4 |
| y2 |
| 3 |
����
|
��C��x1��y1����D��x2��y2������x1+x2=32��x1x2=76��
��|CD|=
| (1+1)(322-4��76) |
| 10 |
���߶�CD�ij���Ϊ12
| 10 |
��2��������ڶ���M���ˣ�0������M��ֱ����˫��������������C��D��
����������ô��תֱ��CD��ʼ��CA��AD��
��ֱ��CD�ķ���Ϊy=k��x-�ˣ���
��C��x3��y3����D��x4��y4����
��A��2��0������kCA=
| y3 |
| x3-2 |
| y4 |
| x4-2 |
��CA��AD����kCA•kAD=
| y3 |
| x3-2 |
| y4 |
| x4-2 |
��������y3y4=-x3x4+2��x3+x4��-4����
��y=k��x-�ˣ���
��y3y4=[k��x3-�ˣ�][k��x4-�ˣ�]
=k2x3x4-k2�ˣ�x3+x4��+k2��2����
�ɢ٢ڣ���k2=-1����=2����������
����������Ķ���M���ˣ�0����
���������⿼���ҳ������������������ĵ��Ƿ���ڵ��жϣ�����ʱҪע����Բ�ҳ���ʽ�ĺ������ã�ע�֤ⷴ���ĺ������ã�

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
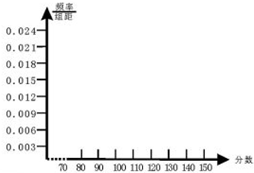 ��ѧϰ��ͳ��ѧ֪ʶ����λͬѧ�������꼶��1200��ͬѧһ����ѧ���Գɼ����������飬��λͬѧ���ü��������������ȡ100��ѧ���ijɼ���������ѡ����ѧ�ɼ��Ƴ���ͳ�Ʊ����豾�ο��Ե������������Ϊ90�֣��ŵ�����ͷ�130�֣����ҿ��Գɼ�������[85��90����ѧ��ͨ������Ŭ���ܴﵽ�������������
��ѧϰ��ͳ��ѧ֪ʶ����λͬѧ�������꼶��1200��ͬѧһ����ѧ���Գɼ����������飬��λͬѧ���ü��������������ȡ100��ѧ���ijɼ���������ѡ����ѧ�ɼ��Ƴ���ͳ�Ʊ����豾�ο��Ե������������Ϊ90�֣��ŵ�����ͷ�130�֣����ҿ��Գɼ�������[85��90����ѧ��ͨ������Ŭ���ܴﵽ������������� ��ͼ��A��B����Բ
��ͼ��A��B����Բ