��Ŀ����
5��ij��ѧ��ѧ��ʦ�ֱ������ֲ�ͬ��ѧ��ʽ����ѧ��ѧƽ���ֺ������ʶ���ͬ�ļס���������һ�°ࣨ������Ϊ20�ˣ����н�ѧ�������ѧ��ѧϰ��ѧ�ڷ̶ܳȺ��Ծ���һ�£�����ѧ���տ��Գɼ���Ҷͼ���£�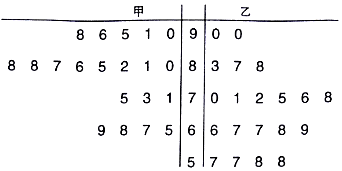
��1��ѧУ�涨���ɼ�������75�ֵ����㣬����д�����2��2���������ж��ж�������Ϊ���ɼ��������ѧ��ʽ�йء���
| �װ� | �Ұ� | �ϼ� | |
| ���� | 14 | 8 | 22 |
| ������ | 6 | 12 | 18 |
| �ϼ� | 20 | 20 | 40 |
| P��x2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
��2������������ѧ�ɼ�������90�ֵ�ͬѧ�������ȡ3�������Ϊ��ȡ�ɼ�������95��ͬѧ��������εķֲ��к�������
���� ��1���ɾ�Ҷͼ�ɵñ�����ɵ�K2�Ľ���ֵ����ϲο���ֵ�ɵý��ۣ�
��2��������ɵæεĿ���ֵ���ֱ��������ʣ��ɵ÷ֲ��У������ɵ���ѧ������
��� �⣺��1����ͼ��ʾ
| �װ� | �Ұ� | �ϼ� | |
| ���� | 14 | 8 | 22 |
| ������ | 6 | 12 | 18 |
| �ϼ� | 20 | 20 | 40 |
��2����������ѧ�ɼ�������90�ֵ�ͬѧ�У��ɼ�������95��ͬѧ������3����
���������ȡ3������=0��1��2��3
$P����=0��=\frac{C_4^3}{C_7^3}=\frac{4}{35}$��$P����=1��=\frac{C_4^2C_3^1}{C_7^3}=\frac{18}{35}$��$P����=2��=\frac{C_4^1C_3^2}{C_7^3}=\frac{12}{35}$��$P����=3��=\frac{C_3^3}{C_7^3}=\frac{1}{35}$��
�εķֲ���Ϊ��
| X | 0 | 1 | 2 | 3 |
| P | $\frac{4}{35}$ | $\frac{18}{35}$ | $\frac{12}{35}$ | $\frac{1}{35}$ |
���� ���⿼�龥Ҷͼ�����ʷֲ��к���ѧ�������Լ������Լ��飬���е��⣮

��ϰ��ϵ�д�
�����Ŀ
16����֪������R�ϵĺ���f��x��=2|x-m|-1��m��R��Ϊż��������a=f��-2����b=f��log25����c=f��2m������a��b��c�Ĵ�С��ϵΪ��������
| A�� | a��b��c | B�� | c��a��b | C�� | a��c��b | D�� | c��b��a |
13��˫����mx2+ny2=1��mn��0����һ�������߷���Ϊ$y=\sqrt{3}x$��������������Ϊ��������
| A�� | 2 | B�� | $\frac{{2\sqrt{3}}}{3}$ | C�� | $\sqrt{3}$��$\frac{{2\sqrt{3}}}{3}$ | D�� | 2��$\frac{{2\sqrt{3}}}{3}$ |
10��ԲE��������A��0��1����B��2��0����C��0��-1������Բ����x����������ϣ���ԲE�ı�����Ϊ��������
| A�� | ��x-$\frac{3}{2}$��2+y2=$\frac{25}{4}$ | B�� | ��x+$\frac{3}{4}$��2+y2=$\frac{25}{16}$ | C�� | ��x-$\frac{3}{4}$��2+y2=$\frac{25}{16}$ | D�� | ��x-$\frac{3}{4}$��2+y2=$\frac{25}{4}$ |
17����֪����A={x|x��3��x��1}��B={x|x2-6x+8��0}����∁RA����B=��������
| A�� | ��1��3�� | B�� | ��1��4�� | C�� | ��2��3�� | D�� | ��2��4�� |
15���ڡ�ABC�У�$AB=3��AC=2��\overrightarrow{BD}=\frac{1}{2}\overrightarrow{BC}����\overrightarrow{AD}•\overrightarrow{DB}$��ֵΪ��������
| A�� | $\frac{5}{2}$ | B�� | $-\frac{5}{2}$ | C�� | $\frac{5}{4}$ | D�� | $-\frac{5}{4}$ |
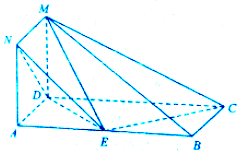 ��ͼ��������ADMN�����ABCD���ڵ�ƽ�����ֱ��AB=2AD=6����EΪ�߶�AB��һ�㣮
��ͼ��������ADMN�����ABCD���ڵ�ƽ�����ֱ��AB=2AD=6����EΪ�߶�AB��һ�㣮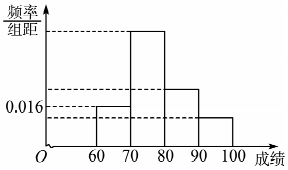 ij��Ϊ�����ѧ��ѧϰӢ�����Ȥ���ڰ��ھ���Ӣ��д��˵�����ۺ�����������������ΪԤ���;���2���Σ�Ԥ��Ϊ���ԣ�����Ϊ˵Ӣ���Ӣ������������вμӱ��Ե�ͬѧ����ͳ�ƣ��õ�Ƶ�ʷֲ�ֱ��ͼ�����к��������θ߶�֮������Ϊ4��2��1������[80��90��������Ϊ12�ˣ�
ij��Ϊ�����ѧ��ѧϰӢ�����Ȥ���ڰ��ھ���Ӣ��д��˵�����ۺ�����������������ΪԤ���;���2���Σ�Ԥ��Ϊ���ԣ�����Ϊ˵Ӣ���Ӣ������������вμӱ��Ե�ͬѧ����ͳ�ƣ��õ�Ƶ�ʷֲ�ֱ��ͼ�����к��������θ߶�֮������Ϊ4��2��1������[80��90��������Ϊ12�ˣ�