题目内容
15.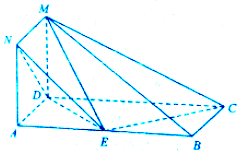 如图,正方形ADMN与矩形ABCD所在的平面相互垂直,AB=2AD=6,点E为线段AB上一点.
如图,正方形ADMN与矩形ABCD所在的平面相互垂直,AB=2AD=6,点E为线段AB上一点.(1)若点E是AB的中点,求证:BM∥平面NDE;
(2)若直线EM与平面所成角的大小为$\frac{π}{6}$,求VE-ADMN:VE-CDM.
分析 (1)连结AM,设AM∩ND=F,连结EF,推导出EF∥BM,由此能证明BM∥平面NDE.
(2)推导出AE=3$\sqrt{2}$,VE-ADMN:VE-CDM=$\frac{1}{3}×AE×{S}_{正方形ADMN}$:$\frac{1}{3}×AD×{S}_{△MDC}$,由此能求出结果.
解答 证明:(1)连结AM,设AM∩ND=F,连结EF,
∵四边形ADMN为正方形,∴F是AM的中点,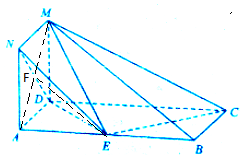
又∵E是AB中点,∴EF∥BM,
∵EF?平面NDE,BM?平面NDE,
∴BM∥平面NDE.
解:(2)∵正方形ADMN与矩形ABCD所在的平面相互垂直,
AB=2AD=6,点E为线段AB上一点.
直线EM与平面所成角的大小为$\frac{π}{6}$,
∴$∠DEM=\frac{π}{6}$,∴ME=6,DE=3$\sqrt{3}$,
AE=$\sqrt{27-9}$=3$\sqrt{2}$,
∴VE-ADMN:VE-CDM=$\frac{1}{3}×AE×{S}_{正方形ADMN}$:$\frac{1}{3}×AD×{S}_{△MDC}$
=$\frac{1}{3}×3\sqrt{2}×{3}^{2}$:$\frac{1}{3}×3×\frac{1}{2}×3×6$
=$\sqrt{2}:1$.
点评 本题考查线面平行的证明,考查两个几何体的比值的求法,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.设函数f(x)=$\left\{\begin{array}{l}{(\frac{1}{3})^{-x}-2,x≥0}\\{2lo{g}_{3}(-x),x<0}\end{array}\right.$若f(m)>1,则m的取值范围是( )
| A. | (1,+∞) | B. | (-$\sqrt{3}$,1) | C. | (-∞,-$\sqrt{3}$)∪(1,+∞) | D. | (-∞,-$\sqrt{3}$) |
3.设?x?表示不小于实数x的最小整数,如?2.6?=3,?-3.5?=-3.已知函数f(x)=?x?2-2?x?,若函数F(x)=f(x)-k(x-2)+2在(-1,4]上有2个零点,则k的取值范围是( )
| A. | $[{-\frac{5}{2},-1})∪[2,5)$ | B. | $({-\frac{4}{3},-1}]∪[5,10)$ | C. | $[{-1,-\frac{2}{3}})∪[5,10)$ | D. | $[{-\frac{4}{3},-1}]∪[5,10)$ |
5.某中学数学老师分别用两种不同教学方式对入学数学平均分和优秀率都相同的甲、乙两个高一新班(人数均为20人)进行教学(两班的学生学习数学勤奋程度和自觉性一致),数学期终考试成绩茎叶图如下:
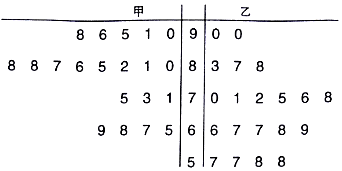
(1)学校规定:成绩不低于75分的优秀,请填写下面的2×2联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
附:参考公式及数据
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
(2)从两个班数学成绩不低于90分的同学中随机抽取3名,设ξ为抽取成绩不低于95分同学人数,求ξ的分布列和期望.

(1)学校规定:成绩不低于75分的优秀,请填写下面的2×2联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
| 甲班 | 乙班 | 合计 | |
| 优秀 | 14 | 8 | 22 |
| 不优秀 | 6 | 12 | 18 |
| 合计 | 20 | 20 | 40 |
| P(x2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)从两个班数学成绩不低于90分的同学中随机抽取3名,设ξ为抽取成绩不低于95分同学人数,求ξ的分布列和期望.