题目内容
16.已知定义在R上的函数f(x)=2|x-m|-1(m∈R)为偶函数,记a=f(-2),b=f(log25),c=f(2m),则a,b,c的大小关系为( )| A. | a<b<c | B. | c<a<b | C. | a<c<b | D. | c<b<a |
分析 根据题意,由于函数为偶函数,则有f(-x)=f(x),即2|x-m|-1=2|-x-m|-1,分析可得m=0,即可得函数f(x)的解析式,结合指数函数的性质可得当x≥0时,函数f(x)为增函数;对于a、b、c三个数,比较自变量绝对值的大小,结合函数的单调性,即可得答案.
解答 解:根据题意,函数f(x)=2|x-m|-1(m∈R)为偶函数,
则有f(-x)=f(x),即2|x-m|-1=2|-x-m|-1,
分析可得m=0,
则f(x)=2|x|-1=$\left\{\begin{array}{l}{{2}^{x}-1,x≥0}\\{{\frac{1}{2}}^{x}-1,x<0}\end{array}\right.$,
分析可得当x≥0时,函数f(x)为增函数;
a=f(-2)=f(2),b=f(log25),c=f(2m)=f(0),
又由0<2<log25,
则有c<a<b;
故选:B.
点评 本题考查函数偶函数的性质,关键是利用偶函数的性质求出m的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.已知△ABC的内角A、B、C的对边分别为a、b、c.若a=bcosC+csinB,且△ABC的面积为1+$\sqrt{2}$.则b的最小值为( )
| A. | 2 | B. | 3 | C. | $\sqrt{2}$ | D. | $\sqrt{3}$ |
8.《九章算术》是我国数学史上堪与欧几里得《几何原本》相媲美的数学名著.其中,将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马;将四个面都为直角三角形的四面体称之为鳖膈.已知直三棱柱A1B1C1-ABC中,AB⊥BC,AB=3,$BC=4,A{A_1}=5\sqrt{3}$,将直三棱柱沿一条棱和两个面的对角线分割为一个阳马和一个鳖膈,则鳖膈的体积与其外接球的体积之比为( )
| A. | $\sqrt{3}:15π$ | B. | $3\sqrt{3}:5π$ | C. | $3\sqrt{3}:50π$ | D. | $3\sqrt{3}:25π$ |
5.某中学数学老师分别用两种不同教学方式对入学数学平均分和优秀率都相同的甲、乙两个高一新班(人数均为20人)进行教学(两班的学生学习数学勤奋程度和自觉性一致),数学期终考试成绩茎叶图如下:
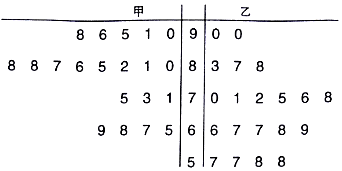
(1)学校规定:成绩不低于75分的优秀,请填写下面的2×2联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
附:参考公式及数据
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
(2)从两个班数学成绩不低于90分的同学中随机抽取3名,设ξ为抽取成绩不低于95分同学人数,求ξ的分布列和期望.

(1)学校规定:成绩不低于75分的优秀,请填写下面的2×2联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
| 甲班 | 乙班 | 合计 | |
| 优秀 | 14 | 8 | 22 |
| 不优秀 | 6 | 12 | 18 |
| 合计 | 20 | 20 | 40 |
| P(x2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)从两个班数学成绩不低于90分的同学中随机抽取3名,设ξ为抽取成绩不低于95分同学人数,求ξ的分布列和期望.
6.“m=1”是“函数f(x)=log2(1+mx)-log2(1-mx)为奇函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |