题目内容
14.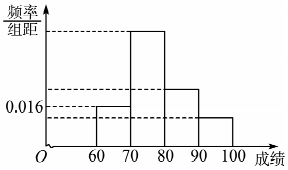 某班为了提高学生学习英语的兴趣,在班内举行英语写、说、唱综合能力比赛,比赛分为预赛和决赛2个阶段,预赛为笔试,决赛为说英语、唱英语歌曲,将所有参加笔试的同学进行统计,得到频率分布直方图,其中后三个矩形高度之比依次为4:2:1,落在[80,90)的人数为12人.
某班为了提高学生学习英语的兴趣,在班内举行英语写、说、唱综合能力比赛,比赛分为预赛和决赛2个阶段,预赛为笔试,决赛为说英语、唱英语歌曲,将所有参加笔试的同学进行统计,得到频率分布直方图,其中后三个矩形高度之比依次为4:2:1,落在[80,90)的人数为12人.(Ⅰ)求此班级人数;
(Ⅱ)按规定预赛成绩不低于90分的选手参加决赛,已知甲乙两位选手已经取得决赛资格,参加决赛的选手按抽签方式决定出场顺序.
(i)甲不排在第一位乙不排在最后一位的概率;
(ii)记甲乙二人排在前三位的人数为X,求X的分布列和数学期望.
分析 (Ⅰ)落在区间[80,90)的频率是(1-0.16)×$\frac{2}{7}$,即可得出人数.
(Ⅱ)由(Ⅰ)知,参加决赛的选手共6人,(i)设“甲不在第一位,乙不在最后一位”为事件A,利用相互独立与互斥事件的概率计算公式即可得出甲不在第一位、乙不在最后一位的概率.
(ii)随机变量的可能取值为0,1,2,利用相互独立事件的概率计算公式即可得出随机变量X的分布列.
解答 解:(Ⅰ)落在区间[80,90)的频率是$(1-0.16)×\frac{2}{7}=0.24$,
所以人数$n=\frac{12}{0.24}=50$.
(Ⅱ)由(Ⅰ)知,参加决赛的选手共6人,
(i)设“甲不在第一位,乙不在最后一位”为事件A,
则$P(A)=\frac{A_5^5+A_4^1A_4^1A_4^4}{A_6^6}=\frac{7}{10}$,
所以甲不在第一位、乙不在最后一位的概率为$\frac{7}{10}$.
(ii)随机变量的可能取值为0,1,2,$P(X=0)=\frac{A_3^2A_4^4}{A_6^6}=\frac{1}{5}$,$P(X=1)=\frac{C_2^1A_3^1A_3^1A_4^4}{A_6^6}=\frac{3}{5}$,$P(X=2)=\frac{A_3^2A_4^4}{A_6^6}=\frac{1}{5}$,
随机变量X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{1}{5}$ | $\frac{3}{5}$ | $\frac{1}{5}$ |
所以随机变量的数学期望为1.
点评 本题考查了相互独立与互斥事件的概率计算公式、随机变量的分布列与数学期望计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.某中学数学老师分别用两种不同教学方式对入学数学平均分和优秀率都相同的甲、乙两个高一新班(人数均为20人)进行教学(两班的学生学习数学勤奋程度和自觉性一致),数学期终考试成绩茎叶图如下:
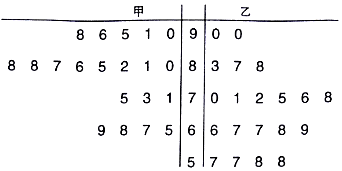
(1)学校规定:成绩不低于75分的优秀,请填写下面的2×2联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
附:参考公式及数据
K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$
(2)从两个班数学成绩不低于90分的同学中随机抽取3名,设ξ为抽取成绩不低于95分同学人数,求ξ的分布列和期望.

(1)学校规定:成绩不低于75分的优秀,请填写下面的2×2联表,并判断有多大把握认为“成绩优秀与教学方式有关”.
| 甲班 | 乙班 | 合计 | |
| 优秀 | 14 | 8 | 22 |
| 不优秀 | 6 | 12 | 18 |
| 合计 | 20 | 20 | 40 |
| P(x2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)从两个班数学成绩不低于90分的同学中随机抽取3名,设ξ为抽取成绩不低于95分同学人数,求ξ的分布列和期望.
9.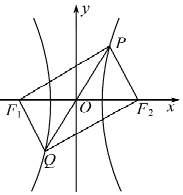 已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0)的左、右焦点,若直线y=2x与双曲线C交于P、Q两点,且四边形PF1QF2是矩形,则双曲线的离心率为( )
已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0)的左、右焦点,若直线y=2x与双曲线C交于P、Q两点,且四边形PF1QF2是矩形,则双曲线的离心率为( )
 已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0)的左、右焦点,若直线y=2x与双曲线C交于P、Q两点,且四边形PF1QF2是矩形,则双曲线的离心率为( )
已知F1,F2是双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0$,b>0)的左、右焦点,若直线y=2x与双曲线C交于P、Q两点,且四边形PF1QF2是矩形,则双曲线的离心率为( )| A. | $5-2\sqrt{5}$ | B. | $5+2\sqrt{5}$ | C. | $\sqrt{5+2\sqrt{5}}$ | D. | $\sqrt{5-2\sqrt{5}}$ |
19.圆:x2+y2+2ax+a2-9=0和圆:x2+y2-4by-1+4b2=0有三条公切线,若a∈R,b∈R,且ab≠0,则$\frac{4}{a^2}+\frac{1}{b^2}$的最小值为( )
| A. | 1 | B. | 3 | C. | 4 | D. | 5 |
6.“m=1”是“函数f(x)=log2(1+mx)-log2(1-mx)为奇函数”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
3.函数y=sin2x的图象向左平移φ(φ>0)个单位后关于直线$x=\frac{π}{3}$对称,则φ的最小值为( )
| A. | $\frac{π}{12}$ | B. | $\frac{5π}{12}$ | C. | $\frac{π}{6}$ | D. | $\frac{5π}{6}$ |
4.$\int_1^e{(x+\frac{1}{x}})dx$=( )
| A. | e2 | B. | $\frac{{{e^2}+1}}{2}$ | C. | $\frac{{{e^2}-1}}{2}$ | D. | $\frac{{{e^2}+3}}{2}$ |



