题目内容
已知命题p：“?x∈R，x2+1＞0”命题q：“?x∈R，tanx=2”，则下列判断正确的是（ ）
| A、p∨q为真，￢p为真 |
| B、p∨q为假，￢p为假 |
| C、p∧q为真，￢p为真 |
| D、p∧q为真，￢p为假 |
考点：复合命题的真假
专题：规律型
分析：先判断命题p和命题q的真假，然后判断￢P和￢q的真假，由此判断复合命题“p∧q”，“p∧￢q”，“￢p∨q”和“￢p∨￢q”的真假．
解答：
解：命题p：“?x∈R，x2+1＞0”，为真命题，则￢p为假命题；
命题q：?x∈R，使tanx=2，为真命题，￢q为假命题；
∴p∨q为真命题￢p为假命题，
故选：D．
命题q：?x∈R，使tanx=2，为真命题，￢q为假命题；
∴p∨q为真命题￢p为假命题，
故选：D．
点评：本题主要考查了命题真假判断的应用，简单复合命题的真假判断，属于基础试题
练习册系列答案
阅读快车系列答案
相关题目
“m＜0”是“方程x2+my2=1表示双曲线”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
在长为8的线段AB上任取一点C，现作一矩形，邻边长分别等于AC、BC的长，则该矩形面积大于15的概率（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
对任意两实数a，b，定义运算“*”：a*b=
，关于函数f（-x）=e-x*ex，给出下列四个结论：
①函数f（x）的最小值是e；
②函数f（x）为偶函数；
③函数f（x）在（0，+∞）上单调递增；
④函数f（x）的图象与直线y=ex没有公共点；
其中正确结论的序号是（ ）
|
①函数f（x）的最小值是e；
②函数f（x）为偶函数；
③函数f（x）在（0，+∞）上单调递增；
④函数f（x）的图象与直线y=ex没有公共点；
其中正确结论的序号是（ ）
| A、①③ | B、②③ | C、①④ | D、②④ |
当实数x，y满足不等式
时，恒有ax+y≤2成立，则实数a的取值集合是（ ）
|
| A、（0，1] |
| B、（-∞，1] |
| C、（-1，1] |
| D、（1，2） |
如图1，△ABC为正三角形，△BCD为等腰直角三角形，∠BCD=90°，将△ABC沿BC边折叠到△A′BC的位置，使A′B=A′D，E为BD中点，如图2．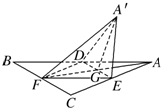
如图，正三角形ABC的中线AF与中位线DE相交于点G，已知△A′ED是△AED绕DE旋转过程中的一个图形，现给出下列四个命题：