题目内容
已知点P(1,m)是函数y=ax+
图象上的点,直线x+y=b是该函数图象在P点处的切线,则a+b-m= .
| 2 |
| x |
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:求出函数y=ax+
的导数,求出切线的斜率,由已知切线,得到a-2=-1,从而得到m,再由切线过切点,即可得到b,进而得到a+b-m.
| 2 |
| x |
解答:
解:点P(1,m)是函数y=ax+
图象上的点,则m=a+2,
函数y=ax+
的导数y′=a-
,
该函数图象在P点处的切线斜率为a-2,
由于直线x+y=b是该函数图象在P点处的切线,
则有a-2=-1,即a=1,m=3,b=1+m=4,
则有a+b-m=1+4-3=2.
故答案为:2.
| 2 |
| x |
函数y=ax+
| 2 |
| x |
| 2 |
| x2 |
该函数图象在P点处的切线斜率为a-2,
由于直线x+y=b是该函数图象在P点处的切线,
则有a-2=-1,即a=1,m=3,b=1+m=4,
则有a+b-m=1+4-3=2.
故答案为:2.
点评:本题考查导数的几何意义:函数在某点处的导数即为曲线在该点处的切线的斜率,考查运算能力,属于基础题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
下列函数中,在区间[0,
]上为减函数的是( )
| π |
| 2 |
| A、y=sinx | ||
| B、y=cosx | ||
| C、y=tanx | ||
D、y=sin(x-
|
抽查10件产品,设事件A:至少有2件次品,则A的对立事件为( )
| A、至多有2件次品 |
| B、至多有1件次品 |
| C、至多有2件正品 |
| D、至多有1件正品 |
如图中的直线l1、l2、l3的斜率分别为k1、k2、k3,则( )
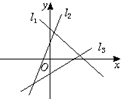

| A、k1<k2<k3 |
| B、k3<k1<k2 |
| C、k3<k2<k1 |
| D、k1<k3<k2 |