题目内容
函数f(x)=
在[-5,-4]上的值域是 .
| 3 |
| x+2 |
考点:函数的值域
专题:函数的性质及应用
分析:求f′(x),根据f′(x)的符号判断f(x)在[-5,-4]上的单调性,根据单调性即可求出f(x)在[-5,-4]上的值域.
解答:
解:f′(x)=-
<0,∴f(x)在[-5,-4]上单调递减;
f(-5)=
=-1,f(-4)=
=-
.∴f(x)∈[-
,-1];
即函数f(x)在[-5,-4]上的值域是[-
,-1].
故答案为:[-
,-1].
| 3 |
| (x+2)2 |
f(-5)=
| 3 |
| -5+2 |
| 3 |
| -4+2 |
| 3 |
| 2 |
| 3 |
| 2 |
即函数f(x)在[-5,-4]上的值域是[-
| 3 |
| 2 |
故答案为:[-
| 3 |
| 2 |
点评:考查根据导数符号判断函数单调性的方法,函数的值域概念及根据函数单调性求函数的值域.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
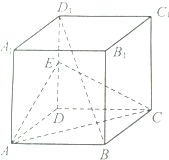 如图,正方体ABCD-A1B1C1D1中,E为DD1的中点.
如图,正方体ABCD-A1B1C1D1中,E为DD1的中点.