题目内容
18. 在△ABC中,∠B=$\frac{π}{6}$,AC=$\sqrt{5}$,D是AB边上一点,CD=2,△ACD的面积为2,∠ACD为锐角,则BC=$\frac{8\sqrt{5}}{5}$.
在△ABC中,∠B=$\frac{π}{6}$,AC=$\sqrt{5}$,D是AB边上一点,CD=2,△ACD的面积为2,∠ACD为锐角,则BC=$\frac{8\sqrt{5}}{5}$.
分析 推导出sin∠ACD=$\frac{2}{\sqrt{5}}$,cos∠ACD=$\frac{\sqrt{5}}{5}$,由余弦定理得AD=$\sqrt{5}$,由正弦定理,得sinA=$\frac{4}{5}$,由此利用正弦定理能求出BC的长.
解答 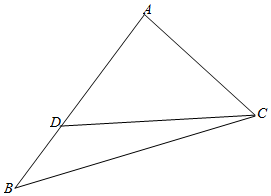 解:∵在△ABC中,∠B=$\frac{π}{6}$,AC=$\sqrt{5}$,D是AB边上一点,CD=2,
解:∵在△ABC中,∠B=$\frac{π}{6}$,AC=$\sqrt{5}$,D是AB边上一点,CD=2,
△ACD的面积为2,∠ACD为锐角,
∴S△ACD=$\frac{1}{2}×2×\sqrt{5}$×sin∠ACD=2,解得sin∠ACD=$\frac{2}{\sqrt{5}}$,
∴cos∠ACD=$\sqrt{1-(\frac{2}{\sqrt{5}})^{2}}$=$\frac{\sqrt{5}}{5}$,
∴AD=$\sqrt{5+4-2×2×\sqrt{5}×cos∠ACD}$=$\sqrt{5}$,
由正弦定理,得:$\frac{2}{sinA}=\frac{\sqrt{5}}{sin∠ACD}$,解得sinA=$\frac{2×\frac{2}{\sqrt{5}}}{\sqrt{5}}$=$\frac{4}{5}$,
又$\frac{BC}{sinA}=\frac{AC}{sinB}$,∴BC=$\frac{ACsinA}{sinB}$=$\frac{\sqrt{5}×\frac{4}{5}}{\frac{1}{2}}$=$\frac{8\sqrt{5}}{5}$.
故答案为:$\frac{8\sqrt{5}}{5}$.
点评 本题考查三角形边长的求法,涉及到正弦定理、余弦定理等基础知识,考查推理论证能力、运算求解能力,考查函数与方思想、数形结合思想,是中档题.

练习册系列答案
相关题目
8.某四棱锥的三视图如图所示,则最长的一条侧棱的长度是( )
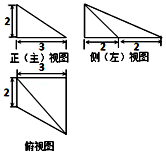

| A. | $2\sqrt{5}$ | B. | $4\sqrt{2}$ | C. | $\sqrt{29}$ | D. | $\sqrt{13}$ |
9.执行如图所示的程序框图,若输出的结果为S=1320,则判断框内应填入的内容是( )


| A. | K<9? | B. | K<10? | C. | K<11? | D. | K<12? |
6.已知过曲线$\left\{\begin{array}{l}{x=3sinθ}\\{y=3cosθ}\end{array}\right.$(θ为参数,0≤θ≤π)上一点P与原点O的直线PO的倾斜角为$\frac{π}{2}$,则P点坐标是( )
| A. | (0,3) | B. | $(-\frac{12}{5},-\frac{12}{5})$ | C. | (-3,0) | D. | $(\frac{12}{5},\frac{12}{5})$ |
13.执行如图所示的程序框图,则输出s的值等于( )
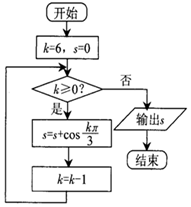

| A. | $-\frac{1}{2}$ | B. | $\frac{1}{2}$ | C. | 0 | D. | 1 |
3.已知函数g(x)=1-cos(πx+ϕ)(0≤ϕ<π)的图象过($\frac{1}{2}$,2),若有4个不同的正数xi满足g(xi)=M(0<M<1),且xi<4(i=1,2,3,4),则从这四个数中任意选出两个,它们的和不超过5的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{2}{3}$ |
10.如图是“二分法”求方程近似解的流程图,在①,②处应填写的内容分别是( )
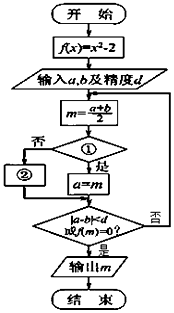

| A. | f(a)•f(m)<0?;b=m | B. | f(b)•f(m)<0?;b=m | C. | f(a)•f(m)<0?;m=b | D. | f(b)•f(m)<0?;b=m |
8.复数$\frac{{(1-i{)^2}}}{3-i}$的值是( )
| A. | $-\frac{1}{4}+\frac{3}{4}i$ | B. | $\frac{1}{4}-\frac{3}{4}i$ | C. | $-\frac{1}{5}+\frac{3}{5}i$ | D. | $\frac{1}{5}-\frac{3}{5}i$ |
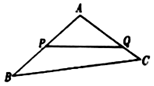 如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.
如图,某生态园将一块三角形地ABC的一角APQ开辟为水果园,已知角A为120°,AB,AC的长度均大于200米,现在边界AP,AQ处建围墙,在PQ处围竹篱笆.