题目内容
13．执行如图所示的程序框图，则输出s的值等于（ ）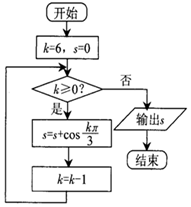
| A． | $-\frac{1}{2}$ | B． | $\frac{1}{2}$ | C． | 0 | D． | 1 |
分析 根据程序框图，进行模拟计算即可．
解答 解：由程序框图得s=cos$\frac{6π}{3}$+cos$\frac{5π}{3}$+cos$\frac{4π}{3}$+cosπ+cos$\frac{2π}{3}$+cos$\frac{π}{3}$+cos0=1+$\frac{1}{2}$-$\frac{1}{2}$-1-$\frac{1}{2}$$+\frac{1}{2}$+1=1，
故选：D
点评 本题主要考查程序框图的应用，根据条件得到S的计算式子是解决本题的关键．
练习册系列答案
名校课堂系列答案
相关题目
1．若f（x）是定义在R上的可导函数，且对任意x∈R，满足f（x）+f'（x）＞0，则对任意实数a，b（ ）
| A． | a＞b?eaf（b）＞ebf（a） | B． | a＞b?eaf（b）＜ebf（a） | C． | a＞b?eaf（a）＜ebf（b） | D． | a＞b?eaf（a）＞ebf（b） |
8．有甲、乙两个班级进行数学考试，按照大于等于120分为优秀，120分以下为非优秀统计成绩后，得到如下2×2列联表：（单位：人）．
已知在全部105人中随机抽取1人成绩是优秀的概率为$\frac{2}{7}$，
（1）请完成上面的2 x×2列联表，并根据表中数据判断，是否有95%的把握认为“成绩与班级有关系”？
（2）若甲班优秀学生中有男生6名，女生4名，现从中随机选派3名学生参加全市数学竞赛，记参加竞赛的男生人数为X，求X的分布列与期望．
附：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
| 优秀 | 非优秀 | 总计 | |
| 甲班 | 10 | ||
| 乙班 | 30 | ||
| 总计 | 105 |
（1）请完成上面的2 x×2列联表，并根据表中数据判断，是否有95%的把握认为“成绩与班级有关系”？
（2）若甲班优秀学生中有男生6名，女生4名，现从中随机选派3名学生参加全市数学竞赛，记参加竞赛的男生人数为X，求X的分布列与期望．
附：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$
| P（K2≥k） | 0.15 | 0.10 | 0.05 | 0.010 |
| k | 2.072 | 2.706 | 3.841 | 6.635 |
在△ABC中，∠B=$\frac{π}{6}$，AC=$\sqrt{5}$，D是AB边上一点，CD=2，△ACD的面积为2，∠ACD为锐角，则BC=$\frac{8\sqrt{5}}{5}$．
5．已知$f（x）=\left\{{\begin{array}{l}{{{log}_{\frac{1}{16}}}（{x+1}），x＜0}\\{-{x^2}+x，x≥0}\end{array}}\right.$，则关于x的方程f（x）=m（m∈R）恰有三个不同的实数根a，b，c，则abc的取值范围是（ ）
| A． | $（{-\frac{1}{16}，0}）$ | B． | $（{-\frac{1}{4}，0}）$ | C． | $（{-\frac{1}{8}，0}）$ | D． | $（{-\frac{1}{2}，0}）$ |
