题目内容

8．某四棱锥的三视图如图所示，则最长的一条侧棱的长度是（　　）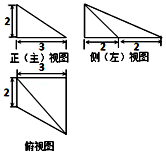
A．$2\sqrt{5}$B．$4\sqrt{2}$C．$\sqrt{29}$D．$\sqrt{13}$

分析 由三视图可知：该几何体为一个四棱锥P-ABCD，其中PA⊥底面ABCD，底面ABCD是直角梯形，AD∥BC，AB=4=2AD，AD⊥AB，PA=2．可得该四棱锥的最长的棱为PC．

解答 解：由三视图可知：该几何体为一个四棱锥P-ABCD，其中PA⊥底面ABCD，
底面ABCD是直角梯形，AD∥BC，AB=4=2AD，AD⊥AB，PA=2．
∴该四棱锥的最长的棱为PC=$\sqrt{{2}^{2}+{3}^{2}+{4}^{2}}$=$\sqrt{29}$．
故选：C．

点评 本题考查了四棱锥的三视图、勾股定理，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
12．下面几种推理是合情推理的是①②④
①由圆的性质类比出球的有关性质；
②由直角三角形、等腰三角形、等边三角形的内角和是180°，归纳出所有三角形的内角和都是180°；
③教室内有一把椅子坏了，则该教室内的所有椅子都坏了；
④三角形内角和是180°，四边形内角和是360°，五边形内角和是540°，由此得出凸多边形的内角和是（n-2）•180°．
13．已知函数f（x）=ax2ex+blnx，且在P（1，f（1））处的切线方程为（3e-1）x-y+1-2e=0，g（x）=（$\frac{2}{x}$-1）ln（x-2）+$\frac{lnx-1}{x}$+1．
（1）求a，b的值；
（2）证明：f（x）的最小值与g（x）的最大值相等．
16．在公差不为0的等差数列{an}中，a22=a3+a6，且a3为a1与a11的等比中项．
（Ⅰ）求数列{an}的通项公式；
（Ⅱ）设bn=（-1）n$\frac{n}{（{a}_{n}-\frac{1}{2}）（{a}_{n+1}-\frac{1}{2}）}$，求数列{bn}的前n项和Tn．
3．已知曲线C1的参数方程为$\left\{\begin{array}{l}x=1+\frac{1}{2}t\\ y=1+\frac{{\sqrt{3}}}{2}t\end{array}\right.$（t是参数），以原点为极点，x轴正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ=2sinθ+4cosθ．
（Ⅰ）求曲线C2的直角坐标方程；
（Ⅱ）判断曲线C1与曲线C2是否相交，若相交，求出交点A，B间的距离，若不想交，请说明理由．
13．在平面直角坐标系中．圆C的参数方程为$\left\{\begin{array}{l}{x=2cosα}\\{y=3+2sinα}\end{array}\right.$（α为参数），以坐标原点为极点，x轴正半轴为极轴建立极坐标系，点D的极坐标为（ρ1，π）．
（1）求圆C的极坐标方程；
（2）过点D作圆C的切线，切点分别为A，B，且∠ADB=60°，求ρ1．
20．已知函数f（x）=|x-2|+|x-4|的最小值为m，正实数a，b满足a+b=m．
（1）求m的值；
（2）求证：$\frac{1}{a}+\frac{1}{b}$≥2．
17．已知函数$f（x）=\sqrt{1+{x^2}}$，x∈R．
（1）证明对?a、b∈R，且a≠b，总有：|f（a）-f（b）|＜|a-b|；
（2）设a、b、c∈R，且$a+b+c=f（2\sqrt{2}）$，证明：a+b+c≥ab+bc+ca．
18．在△ABC中，∠B=$\frac{π}{6}$，AC=$\sqrt{5}$，D是AB边上一点，CD=2，△ACD的面积为2，∠ACD为锐角，则BC=$\frac{8\sqrt{5}}{5}$．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网