Question

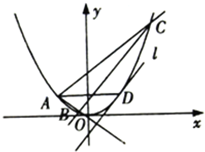已知A，B，C，D是曲线y=x²上的四点，且A，D关于曲线的对称轴对称，直线BC与曲线在点D处的切线平行
（1）证明：直线AC与直线AB的倾斜角互补
（2）设D到直线AB，AC的距离分别为d₁，d₂，若d₁+d₂=

2

|AD|，且△ABC的面积为3，求点A坐标及直线BC的方程．

Answer 1

考点：直线与圆锥曲线的关系,直线的斜率

专题：圆锥曲线的定义、性质与方程

分析：（1）设B（x₁，y₁），C（x₂，y₂），A（a，a²），D（-a，a²）．利用导数的几何意义和斜率计算公式可得x₁+x₂=-2a．同理k_AC=x₁+a，k_AB=x₂+a，即可证明k_AC+k_AB=0．
（2）由于直线AC与直线AB的倾斜角互补，且AD∥x轴，可得AD平分∠CAB．于是d₁=d₂.sin∠DAC=

d1

|AD|

=

2

2

．∠DAC=45°．设k_AC=1，则k_AB=-1．得到△ABC为直角三角形．进而得到|AB|=

2

•|x1-a|=

2

|2a+1|，|AC|=

2

|2a-1|，再利用三角形的面积计算公式S_△ABC=

1

2

|AB|•|AC|=

1

2

×2×|2a+1| |2a-1|=3，即可解得a的值．

解答： 证明：（1）设B（x₁，y₁），C（x₂，y₂），A（a，a²），D（-a，a²）．
∵y=x²，∴y′=2x．∴

y

′ D

=-2a．
又kBC=

y1-y2

x1-x2

=

x 2 1 - x 2 2

x1-x2

=x₁+x₂．
∴x₁+x₂=-2a．
同理k_AC=x₁+a，k_AB=x₂+a，
∴k_AC+k_AB=x₁+x₂+2a=0．
∴直线AC与直线AB的倾斜角互补．
（2）解：∵直线AC与直线AB的倾斜角互补，且AD∥x轴，
∴AD平分∠CAB．
∴d₁=d₂．
∴2d1=

2

|AD|，sin∠DAC=

d1

|AD|

=

2

2

．
∴∠DAC=45°．
设k_AC=1，则k_AB=-1．
∴△ABC为直角三角形．
∵x₁+a=-1，x₂+a=1．
∴|AB|=

2

•|x1-a|=

2

|2a+1|，|AC|=

2

|2a-1|，
∴S_△ABC=

1

2

|AB|•|AC|=

1

2

×2×|2a+1| |2a-1|=3，
解得a=1或-1．
当a=-1时，A（-1，1），直线BC的方程为y=2x．
当a=1时，A（1，1），直线BC的方程为y=-2x．

点评：本题综合考查了直线与抛物线的位置关系、斜率计算公式、导数的几何意义、角平分线的性质、直角三角形的边角关系、三角形的面积计算公式、直线的方程等基础知识与基本技能方法，考查了推理能力和计算能力，考查了数形结合的能力，属于难题．