题目内容
△ABC的三个内角A,B,C所对的边分别为a,b,c,向量
=(2,-2),向量
=(cosBcosC,sinBsinC-
),且
⊥
.
(Ⅰ)求A的大小;
(Ⅱ)若a=2,△ABC为钝角三角形,且2sin2C+
sin2C-1-
=0,求△ABC的面积.
| m |
| n |
| ||
| 2 |
| m |
| n |
(Ⅰ)求A的大小;
(Ⅱ)若a=2,△ABC为钝角三角形,且2sin2C+
| 3 |
| 3 |
考点:余弦定理,平面向量数量积的运算,正弦定理
专题:三角函数的求值
分析:(Ⅰ)由两向量的坐标,以及两向量垂直时数量积为0列出关系式,求出cosA的值,即可确定出A的大小;
(Ⅱ)已知等式利用二倍角的余弦函数公式化简,整理后利用两角和与差的正弦函数公式变形,求出C的度数,由A的度数求出B的度数,求出三角形面积即可.
(Ⅱ)已知等式利用二倍角的余弦函数公式化简,整理后利用两角和与差的正弦函数公式变形,求出C的度数,由A的度数求出B的度数,求出三角形面积即可.
解答:
 解:(Ⅰ)∵向量
解:(Ⅰ)∵向量
=(2,-2),向量
=(cosBcosC,sinBsinC-
),且
⊥
,
∴2cosBcosC-2sinBsinC+
=0,即cos(B+C)=-cosA=-
,
∴cosA=
,
则A=
;
(Ⅱ)2sin2C+
sin2C-1-
=
sin2C-cos2C-
=0,
变形得:sin(2C-
)=
,
∴2C-
=
或2C-
=
,
即C=
或C=
,
当C=
时,A=
,B=
,符合题意,
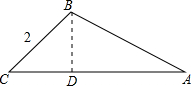
如图所示,BC=a=2,
在Rt△BCD中,∠C=
,
∴BD=CD=
,
在Rt△ABD中,BD=
,∠A=
,
∴AB=2
,AD=
,
此时△ABC面积为
AC•BD=
×(
+
)×
=1+
;
当C=
时,A=
,B=
,不合题意,舍去,
则△ABC的面积为1+
.
 解:(Ⅰ)∵向量
解:(Ⅰ)∵向量| m |
| n |
| ||
| 2 |
| m |
| n |
∴2cosBcosC-2sinBsinC+
| 3 |
| ||
| 2 |
∴cosA=
| ||
| 2 |
则A=
| π |
| 6 |
(Ⅱ)2sin2C+
| 3 |
| 3 |
| 3 |
| 3 |
变形得:sin(2C-
| π |
| 6 |
| ||
| 2 |
∴2C-
| π |
| 6 |
| π |
| 3 |
| π |
| 6 |
| 2π |
| 3 |
即C=
| π |
| 4 |
| 5π |
| 12 |
当C=
| π |
| 4 |
| π |
| 6 |
| 7π |
| 12 |
如图所示,BC=a=2,
在Rt△BCD中,∠C=
| π |
| 4 |
∴BD=CD=
| 2 |
在Rt△ABD中,BD=
| 2 |
| π |
| 6 |
∴AB=2
| 2 |
| 6 |
此时△ABC面积为
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 6 |
| 2 |
| 3 |
当C=
| 5π |
| 12 |
| π |
| 6 |
| 5π |
| 12 |
则△ABC的面积为1+
| 3 |
点评:此题考查了正弦、余弦定理,平面向量的数量积运算,以及三角形面积公式,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目
若(x+
)n展开式中第32项与第72项的系数相同,那么展开式的最中间一项的系数为( )
| 1 |
| x |
A、C
| ||
B、C
| ||
C、C
| ||
D、C
|
 如图,D是直角△ABC斜边BC上一点,AB=AD,记∠CAD=α,∠ACB=β.
如图,D是直角△ABC斜边BC上一点,AB=AD,记∠CAD=α,∠ACB=β.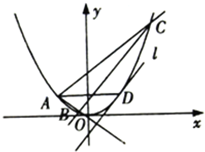 已知A,B,C,D是曲线y=x2上的四点,且A,D关于曲线的对称轴对称,直线BC与曲线在点D处的切线平行
已知A,B,C,D是曲线y=x2上的四点,且A,D关于曲线的对称轴对称,直线BC与曲线在点D处的切线平行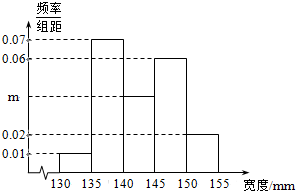 1895年,在伦敦有100块男性头盖骨被挖掘出土,经考证,头盖骨的主人死于1665-1666年之间的大瘟疫.人类学家分别测量了这些头盖骨的宽度,得到的频率分布直方图如图所示.
1895年,在伦敦有100块男性头盖骨被挖掘出土,经考证,头盖骨的主人死于1665-1666年之间的大瘟疫.人类学家分别测量了这些头盖骨的宽度,得到的频率分布直方图如图所示.