题目内容
函数f(x)=
的图象大致是( )
| x2-1 |
| e|x| |
A、 |
B、 |
C、 |
D、 |
考点:函数的图象
专题:函数的性质及应用
分析:易知定义域x∈R,然后根据图象判断奇偶性,易知f(-x)=
=f(x),是偶函数,排除B;再结合当x→+∞时,f(x)>0排除D;对于A、B可以看出,A无极值点,只需对函数求当x>0时的导数,判断f′(x)=0是否有解,并判断其是否是极值点即可.
| x2-1 |
| e|x| |
解答:
解:∵x∈R,且f(-x)=f(x)
∴f(x)是偶函数,故排除B项;
又∵x→+∞时,f(x)→+∞,所以排除D项;
而x>0时,令f′(x)=
=0得
x=1-
或1+
,且1-
<x<1+
时f′(x)>0;x>1+
时,f′(x)<0.
∴x=1+
是原函数的极大值点.
故选C
∴f(x)是偶函数,故排除B项;
又∵x→+∞时,f(x)→+∞,所以排除D项;
而x>0时,令f′(x)=
| -x2+2x+1 |
| ex |
x=1-
| 2 |
| 2 |
| 2 |
| 2 |
| 2 |
∴x=1+
| 2 |
故选C
点评:这种题型一般从函数的奇偶性、单调性、极值、特殊点及函数值的变化趋势等几方面入手分析,结合排除法、特殊值法等方法解决问题.

练习册系列答案
相关题目
若抛物线y2=-2px(p>0)的准线为圆x2+y2=4的切线,则P=( )
| A、2 | B、8 | C、6 | D、4 |
用数学归纳法证明1+2+3+…+n3=
,则当n=k+1时,左端应在n=k的基础上加上( )
| n6+n3 |
| 2 |
| A、k3+1 | ||
| B、(k+1)3 | ||
C、
| ||
| D、(k3+1)+(k3+2)+(k3+3)+…+(k3+1)3 |
如图所示的程序框图,若输入的n的值为1,则输出的k的值为( )


| A、2 | B、3 | C、4 | D、5 |
已知函数f(x)=
,则不等式f(a2-4)>f(3a)的解集为( )
|
| A、(2,6) |
| B、(-1,4) |
| C、(1,4) |
| D、(-3,5) |
“1≤x≤3”是“x2-2x-3≤0”的成立的什么条件?答( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
若(x+
)n展开式中第32项与第72项的系数相同,那么展开式的最中间一项的系数为( )
| 1 |
| x |
A、C
| ||
B、C
| ||
C、C
| ||
D、C
|
在?ABCD中,错误的式子是( )
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|
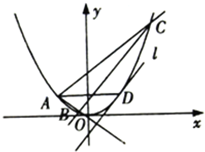 已知A,B,C,D是曲线y=x2上的四点,且A,D关于曲线的对称轴对称,直线BC与曲线在点D处的切线平行
已知A,B,C,D是曲线y=x2上的四点,且A,D关于曲线的对称轴对称,直线BC与曲线在点D处的切线平行