题目内容
20.已知ab=$\frac{1}{4}$,a,b∈(0,1),则$\frac{1}{1-a}$+$\frac{2}{1-b}$的最小值为4+$\frac{4\sqrt{2}}{3}$.分析 先根据条件消掉b,即将b=$\frac{1}{4a}$代入原式得$\frac{1}{1-a}$+$\frac{8a}{4a-1}$,再裂项并用贴“1”法,最后运用基本不等式求其最小值.
解答 解:因为ab=$\frac{1}{4}$,所以,b=$\frac{1}{4a}$,
因此,$\frac{1}{1-a}$+$\frac{2}{1-b}$=$\frac{1}{1-a}$+$\frac{2}{1-\frac{1}{4a}}$
=$\frac{1}{1-a}$+$\frac{8a}{4a-1}$=$\frac{1}{1-a}$+$\frac{2(4a-1)+2}{4a-1}$
=$\frac{1}{1-a}$+$\frac{2}{4a-1}$+2=2($\frac{1}{4a-1}$+$\frac{2}{4-4a}$)+2
=$\frac{2}{3}$($\frac{1}{4a-1}$+$\frac{2}{4-4a}$)[(4a-1)+(4-4a)]+2
=$\frac{2}{3}$[1+2+$\frac{4-4a}{4a-1}$+$\frac{2(4a-1)}{4-4a}$]+2
≥$\frac{2}{3}$(3+2$\sqrt{2}$)+2=4+$\frac{4\sqrt{2}}{3}$,
当且仅当:a=$\frac{1+2\sqrt{2}}{4+2\sqrt{2}}$,取“=”,
即,$\frac{1}{1-a}$+$\frac{2}{1-b}$的最小值为:4+$\frac{4\sqrt{2}}{3}$,
故答案为:4+$\frac{4\sqrt{2}}{3}$.
点评 本题主要考查了基本不等式在求最值问题中的应用,涉及消元,裂项,凑配,贴1等恒等变形,以及取等条件的确定,属于难题.

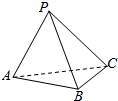
| A. | AP⊥PB,AP⊥PC | B. | AP⊥PB,BC⊥PB | ||
| C. | 平面BPC⊥平面APC,BC⊥PC | D. | AP⊥平面PBC |
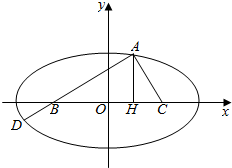 如图,B(-c,0),C(c,0),AH⊥BC,垂足为H,且$\overrightarrow{BH}$=3$\overrightarrow{HC}$.又$\overrightarrow{AD}$=-4$\overrightarrow{DB}$,且A、D同在B、C为焦点的椭圆上,求椭圆的离心率.
如图,B(-c,0),C(c,0),AH⊥BC,垂足为H,且$\overrightarrow{BH}$=3$\overrightarrow{HC}$.又$\overrightarrow{AD}$=-4$\overrightarrow{DB}$,且A、D同在B、C为焦点的椭圆上,求椭圆的离心率.