题目内容
12.如图,在三棱锥P-ABC中,不能证明AP⊥BC的条件是( )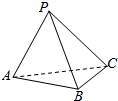
| A. | AP⊥PB,AP⊥PC | B. | AP⊥PB,BC⊥PB | ||
| C. | 平面BPC⊥平面APC,BC⊥PC | D. | AP⊥平面PBC |
分析 利用线面垂直的判定与性质,即可得出结论.
解答 解:对于A,AP⊥PB,AP⊥PC,PB∩PC=P,则AP⊥平面PBC,∴AP⊥BC,不合题意;
对于B,AP⊥PB,BC⊥PB,不能证明AP⊥BC,合题意;
对于C,平面BPC⊥平面APC,平面BPC∩平面APC=PC,BC⊥PC,∴BC⊥平面PAC,∴BC⊥AP,不合题意;
对于D,AP⊥平面PBC,∴AP⊥BC,不合题意;
故选:B.
点评 本题考查线面垂直的判定与性质,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
2.已知α是第四象限角tanα=-$\frac{5}{12}$,则cosα=( )
| A. | $\frac{1}{5}$ | B. | -$\frac{1}{5}$ | C. | $\frac{12}{13}$ | D. | -$\frac{12}{13}$ |
3.设f(x)可导,F(x)=f(x)(1+|sinx|),则f(0)=0是F(x)在x=0处可导的( )
| A. | 充分必要条件 | B. | 充分条件但非必要条件 | ||
| C. | 必要条件但非充分条件 | D. | 既非充分条件又非必要条件 |
7.定义在R上的函数y=f(x)关于y轴对称,且在[0,+∞)上是增加的,则下列关系成立的是( )
| A. | f(3)<f(-4)<f(-π) | B. | f(-π)<f(-4)<f(3) | C. | f(-4)<f(-π)<f(3) | D. | f(3)<f(-π)<f(-4) |
4.执行如图所示的程序框图.若输出的S=$\frac{1023}{512}$,则判断框内的条件可以为( )


| A. | i<10? | B. | i≤10? | C. | i<11? | D. | i≤11? |